【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

参考答案:
【答案】解:(1)∵D(-8,0),∴B点的横坐标为-8,代入![]() 中,得y=-2.
中,得y=-2.
∴B点坐标为(-8,-2).而A、B两点关于原点对称,∴A(8,2).
从而![]() .
.
(2)∵N(0,-n),B是CD的中点,A、B、M、E四点均在双曲线上,
∴![]() ,B(-2m,-
,B(-2m,-![]() ),C(-2m,-n),E(-m,-n).
),C(-2m,-n),E(-m,-n).
S矩形DCNO![]() ,S△DBO=
,S△DBO=![]() ,S△OEN =
,S△OEN =![]() ,
,
∴S四边形OBCE= S矩形DCNO-S△DBO- S△OEN=k.∴![]() .
.
由直线![]() 及双曲线
及双曲线![]() ,得A(4,1),B(-4,-1),
,得A(4,1),B(-4,-1),
∴C(-4,-2),M(2,2).
设直线CM的解析式是![]() ,由C、M两点在这条直线上,得
,由C、M两点在这条直线上,得
![]() 解得
解得![]() .
.
∴直线CM的解析式是![]() .
.
(3)如图,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1.

设A点的横坐标为a,则B点的横坐标为-a.于是
![]() .
.
同理![]() ,
,
∴![]() .
.
【解析】(1)根据B点的横坐标为-8,代入![]() 中,得
中,得![]() ,得出B点的坐标,即可得出A点的坐标,再根据
,得出B点的坐标,即可得出A点的坐标,再根据![]() 求出即可;
求出即可;
- 根据
 ,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.
,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.
分别作![]() ⊥
⊥![]() 轴,
轴,![]() ⊥
⊥![]() 轴,垂足分别为
轴,垂足分别为![]() ,设A点的横坐标为
,设A点的横坐标为![]() ,则B点的横坐标为
,则B点的横坐标为![]() ,于是
,于是![]() ,同理
,同理![]() ,即可得到结果。
,即可得到结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求四边形AEMF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)
我们知道“在数轴上表示的两个数,右边的数总比左边的数大”,利用此规律,我们可以求数轴上两个点之间的距离,具体方法是:用右边的数减去左边的数的差就是表示这两个数的两点之间的距离.若点
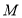 表示的数是
表示的数是 ,点
,点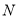 表示的数是
表示的数是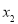 ,点
,点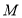 在点
在点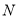 的右边(即
的右边(即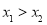 ),则点
),则点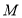 ,
,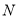 之间的距离为
之间的距离为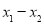 (即
(即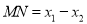 ).
).例如:若点
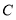 表示的数是-6,点
表示的数是-6,点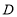 表示的数是-9,则线段
表示的数是-9,则线段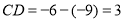 .
.(理解应用)
(1)已知在数轴上,点
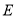 表示的数是-2020,点
表示的数是-2020,点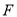 表示的数是2020,求线段
表示的数是2020,求线段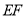 的长;
的长;(拓展应用)
如图,数轴上有三个点,点
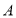 表示的数是-2,点
表示的数是-2,点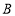 表示的数是3,点
表示的数是3,点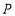 表示的数是
表示的数是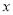 .
.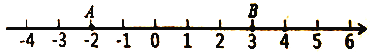
(2)当
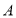 ,
,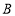 ,
,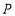 三个点中,其中一个点是另外两个点所连线段的中点时,求
三个点中,其中一个点是另外两个点所连线段的中点时,求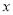 的值;
的值;(3)在点
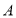 左侧是否存在一点
左侧是否存在一点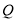 ,使点
,使点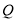 到点
到点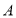 ,点
,点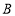 的距离和为19?若存在,求出点
的距离和为19?若存在,求出点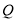 表示的数:若不存在,请说明理由.
表示的数:若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…依此类推,则a2020的值为( )
A.
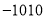 B.
B.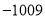 C.
C.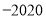 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式:
 ,并把它的解集表示在数轴上;
,并把它的解集表示在数轴上;(2)解不等式组
 ,并写出它的所有非负整数解.
,并写出它的所有非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知CE⊥AB,BF⊥AC,垂足分別为E、F,CE与BF相交于点D,且AD平分∠BAC.求证:CE=BF.
(2)如图2,AD是△ABC的角平分线,AE=AC,EF∥BC交AC于F点,求证:EC平分∠DEF.

-
科目: 来源: 题型:
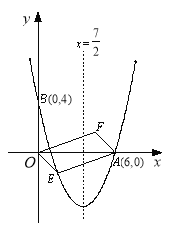
查看答案和解析>>【题目】如图,对称轴为直线x=
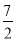 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
相关试题

