【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.

(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
参考答案:
【答案】(1)见解析;(2)4.
【解析】试题分析:(1)由平行线的性质可得:∠A=∠FCE,再根据对顶角相等以及全等三角形的判定方法即可证明:△ADE≌△CFE;
(2)由AB∥FC,可证明△GBD∽△GCF,根据给出的已知数据可求出CF的长,即AD的长,进而可求出AB的长.
(1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
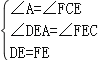 ,
,
∴△ADE≌△CFE(AAS);
(2)解:∵AB∥FC,
∴△GBD∽△GCF,
∴GB:GC=BD:CF,
∵GB=2,BC=4,BD=1,
∴2:6=1:CF,
∴CF=3,
∵AD=CF,
∴AB=AD+BD=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,某市采用价格调控手段达到省电目的.该市电费收费标准如下表(按月结算) :
每月用电量/度
电价/(元/度)
不超过
 度的部分
度的部分 元/度
元/度超过
 度且不超过
度且不超过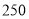 度的部分
度的部分 元/度
元/度超过
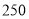 度的部分
度的部分 元/度
元/度解答下列问题:
(1)某居民
 月份用电量为
月份用电量为 度,请问该居民
度,请问该居民 月应缴电费多少元?
月应缴电费多少元?(2)设某月的用电量为
 度
度 ,试写出不同用电量范围应缴的电费(用
,试写出不同用电量范围应缴的电费(用 表示) .
表示) .(3)某居民
 月份缴电费
月份缴电费 元,求该居民
元,求该居民 月份的用电量.
月份的用电量. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国的国球是乒乓球,世界上乒乓球板的拍形大体上可以归为三类:圆形、方形和异形,绝大多数的横板与中国式的直板都是圆型的.如图,李明同学自制一块乒乓球拍,正面是半径为8 cm的⊙O,弧AB的长为4πcm,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为( )

A. (32+48π)cm2 B. (16π﹣32)cm2 C. 64πcm2 D. (48π﹣32)cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD。理由如下:

∵∠1=∠2(已知)
且∠1=∠4( )
∴∠2=∠4(等量代换)
∴CE∥BF( )
∴∠ =∠BFD( )
又∵∠B=∠C(已知)
∴ (等量代换)
∴AB∥CD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校实施新课程改革以来,学生的学习能力有了很大提高,王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图①②).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了________名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比函数y=-
 和y=
和y= (m>0)的图象上.
(m>0)的图象上.
(1)当AB=BC时,求m的值。
(2)连结OA,OD.当OD平方∠AOC时,求△AOD的周长.

相关试题

