【题目】(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?
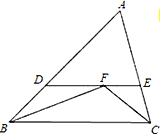
(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?
证明你的猜想。

参考答案:
【答案】(1)成立,证明见解析.(2)证明见解析.
【解析】试题分析: ![]() 根据平行线的性质和角平分线的性质,得出
根据平行线的性质和角平分线的性质,得出![]() 和
和![]() 是等腰三角形,通过等量代换即可得出结论.
是等腰三角形,通过等量代换即可得出结论.
![]() 同
同![]() ,只要求出
,只要求出![]() 和
和![]() 是等腰三角形即可.
是等腰三角形即可.
试题解析:(1)成立;
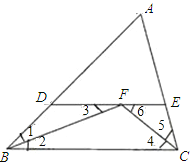
∵△ABC中BF、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠4.
∵DE∥BC,∴∠2=∠3,∠4=∠6.
∴∠1=∠3,∠6=∠5.
根据在同一个三角形中,等角对等边的性质,可知:BD=DF,EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC,
∴∠DBF=∠FBC.
![]()
∴∠DFB=∠FBC.
∴∠ABF=∠DFB,
∴BD=DF.
∵CF平分∠ACG,
∴∠ACF=∠FCG.
![]()
∴∠DFC=∠FCG.
∴∠ACF=∠DFC,
∴CE=EF.
∴EF+DE=DF,即DE+EC=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AC和AB上的点,BD与CE相交于点O,给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.

(1)上述四个条件中,由哪两个条件可以判定AB=AC?(用序号写出所有的情形)
(2)选择(1)小题中的一种情形,说明AB=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张去水果市场购买苹果和桔子,他看中了 A 、B 两家的苹果和桔子,这两家的苹果和桔子的品质都一样,售价也相同,但每千克苹果要比每千克桔子多 12 元,买 2 千克苹果与买 5 千克桔子的费用相等.
(1)根据题意列出方程;
(2)在 x=6,x=7,x=8 中,哪一个是(1)中所列方程的解;
(3)经洽谈,A 家优惠方案是:每购买 10 千克苹果,送 1 千克桔子;B 家优惠方案是:若购买苹果超过 5 千克,则购买桔子打八折,设每千克桔子 x 元, 假设小张购买 30 千克苹果和 a 千克桔子(a>5).
①请用含 a 的式子分别表示出小张在 A、B 两家购买苹果和桔子所花的费用;
②若 a=16,你认为在哪家购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=
 ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,对于任意的x都成立
,对于任意的x都成立求(1)a0的值
(2)a0﹣a1+a2﹣a3+a4﹣a5的值
(3)a2+a4的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使点P到OA,OB的距离都等于a,作法如下:
①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与NM交于点P;④点P即为所求.其中③的依据是( )

A. 平行线之间的距离处处相等 B. 角的内部到角的两边的距离相等的点在角的平分线上
C. 角的平分线上的点到角的两边的距离相等 D. 线段垂直平分线上的点到线段两端点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】有5张背面完全相同的卡片,正面分别写有
 ,(
,(  )0 ,
)0 ,  ,π,2﹣2 . 把卡片背面朝上洗匀后,从中随机抽取1张,其正面的数字是无理数的概率是 .
,π,2﹣2 . 把卡片背面朝上洗匀后,从中随机抽取1张,其正面的数字是无理数的概率是 .
相关试题

