搜索
【题目】设A=2x2+x，B=kx2-（3x2-x+1）.
（1）当x= -1时，求A的值；
（2）小明认为不论k取何值，A-B的值都无法确定.小红认为k可以找到适当的数，使代数式A-B的值是常数.你认为谁的说法正确？请说明理由.
参考答案：
【答案】（1）A=1；（2）小红的说法正确，理由见解析.
【解析】试题（1）把x=-1代入A进行计算即可得；
（2）先计算出A-B，根据结题即可得.
试题解析：（1）当x=-1时，A=2x2+x=2×（-1）2+（-1）=2-1=1；
（2）小红的说法正确，理由如下：
A-B=（2x2+x）-[kx2-(3x2-x+1)]=（5-k）x2+1，
所以当k=5时，A-B=1，
所以小红的说法是正确的.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC内一点P满足PA=PB=PC，则点P一定是△ABC（ ）
A. 三条角平分线的交点 B. 三条中线的交点
C. 三条高的交点 D. 三边垂直平分线的交点
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知m、n是关于x的方程x2+2x﹣1=0的两个不相等的实数根，则m+n=______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知任意三角形的三边长，如何求三角形面积？
古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
（其中a，b，c是三角形的三边长，p=
，S为三角形的面积），并给出了证明例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：
∵a=3，b=4，c=5
∴p=
=6∴S=
=
=6事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．
如图，在△ABC中，BC=5，AC=6，AB=9
（1）用海伦公式求△ABC的面积；
（2）求△ABC的内切圆半径r．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中正确的是（ ）
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形 -
科目： 来源： 题型：
查看答案和解析>>【题目】对于3x－2x+3y－4xy－5,小糊涂同学说了四句话，其中不正确的是（ ）.
A. 是一个整式 B. 由4个单项式组成 C. 次数是2 D. 常数项是－5
-
科目： 来源： 题型：
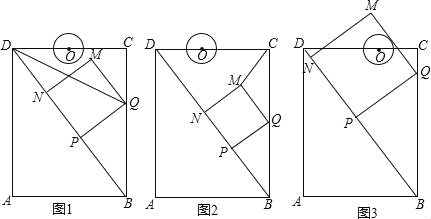
查看答案和解析>>【题目】如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3m/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜）．
（1）如图1，连接DQ平分∠BDC时，t的值为 ；
（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；
（3）请你继续进行探究，并解答下列问题：
①证明：在运动过程中，点O始终在QM所在直线的左侧；
②如图3，在运动过程中，当QM与⊙O相切时，求t的值；并判断此时PM与⊙O是否也相切？说明理由．
相关试题
