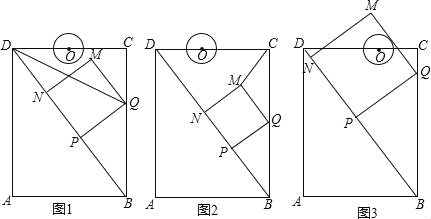
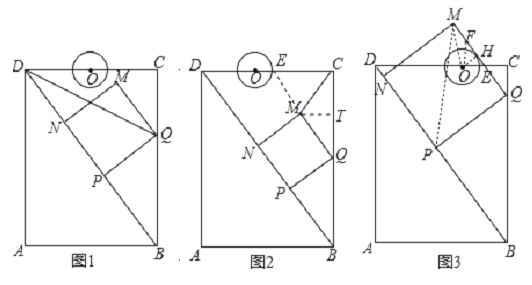
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<).
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
参考答案:
【答案】(1);(2);(3)①证明见解析,②t=,PM与⊙O不相切.
【解析】
试题分析:(1)先证△PBQ∽△CBD,求出PQ、BQ,进而可求出t值;(2)先证△QTM∽△BCD,利用线段成比例可求出t值;(3)①QM交CD于E,利用DE、DO差值比较可判断点O始终在QM所在直线的左侧;②由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.由△OHE∽△BCD,利用线段成比例可求t值,再利用反证法证明直线PM不可能与⊙O相切.
试题解析:解:(1)如图1中,在矩形ABCD中,∠A=∠C=∠ADC=∠ABC=90°,AB=CD=6.AD=BC=8,∴![]() ,∵PQ⊥BD,∴∠BPQ=90°,∵∠PBQ=∠DBC,∠BPQ=∠C,∴△PBQ∽△CBD,∴==,∴==,∴PQ=3t,BQ=5t,∵DQ平分∠BDC,QP⊥DB,QC⊥DC,∴QP=QC,∴3t=6﹣5t,
,∵PQ⊥BD,∴∠BPQ=90°,∵∠PBQ=∠DBC,∠BPQ=∠C,∴△PBQ∽△CBD,∴==,∴==,∴PQ=3t,BQ=5t,∵DQ平分∠BDC,QP⊥DB,QC⊥DC,∴QP=QC,∴3t=6﹣5t,
∴t=.(2)解:如图2中,作MT⊥BC于T.∵MC=MQ,MT⊥CQ,∴TC=TQ,∴ TQ=(8﹣5t),QM=3t,
∵MQ∥BD,∴∠MQT=∠DBC,∵∠MTQ=∠BCD=90°,∴△QTM∽△BCD,∴=,∴
∴t=(s),∴t=s时,△CMQ是以CQ为底的等腰三角形.(3)①证明:如图2中,由此QM交CD于E,
∵EQ∥BD,∴=,∴EC=(8﹣5t),ED=DC﹣EC=6﹣(8﹣5t)=t,∵DO=3t,∴DE﹣DO=t﹣3t=t>0,∴点O在直线QM左侧.②解:如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.∵EC=(8﹣5t),DO=3t,∴OE=6﹣3t﹣(8﹣5t)=t,∵OH⊥MQ,∴∠OHE=90°,∵∠HEO=∠CEQ,
∴∠HOE=∠CQE=∠CBD,∵∠OHE=∠C=90°,∴△OHE∽△BCD,∴=,∴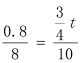 ,∴t=.
,∴t=.
∴t=s时,⊙O与直线QM相切.连接PM,假设PM与⊙O相切,则∠OMH= PMQ=22.5°,在MH上取一点F,使得MF=FO,则∠FMO=∠FOM=22.5°,∴∠OFH=∠FOH=45°,∴OH=FH=0.8,FO=FM=0.8 ,∴MH=0.8(+1),
由=得到HE=,由=得到EQ=,∴MH=MQ﹣HE﹣EQ=4- - =,
∴0.8(+1)≠,矛盾,∴假设不成立.∴直线MQ与⊙O不相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A=2x2+x,B=kx2-(3x2-x+1).
(1)当x= -1时,求A的值;
(2)小明认为不论k取何值,A-B的值都无法确定.小红认为k可以找到适当的数,使代数式A-B的值是常数.你认为谁的说法正确?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】对于3x-2x+3y-4xy-5,小糊涂同学说了四句话,其中不正确的是( ).
A. 是一个整式 B. 由4个单项式组成 C. 次数是2 D. 常数项是-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在线段AB的垂直平分线上,PA=7,则PB=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求
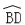 的长(结果保留π).
的长(结果保留π).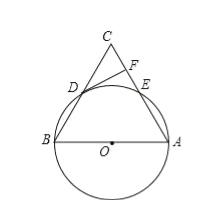
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

相关试题

