【题目】已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B点的坐标为____________;
参考答案:
【答案】(﹣2,2)或(8,2)
【解析】试题分析:根据B点位置分类讨论求解.
解:已知AB∥x轴,点B的纵坐标与点A的纵坐标相同,都是2;
在直线AB上,过点A向左5单位得(﹣2,2),过点A向右5单位得(8,2).
∴满足条件的点有两个:(﹣2,2),(8,2).故答案填:(﹣2,2)或(8,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
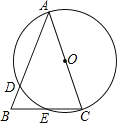
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你写出一个有一根为1的一元二次方程: .(答案不唯一)
-
科目: 来源: 题型:
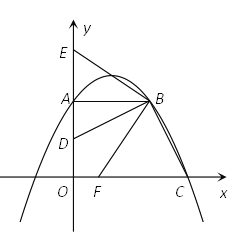
查看答案和解析>>【题目】如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连结EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“350亿”这个数用科学计数法表示为_______________;数”13.14万”精确到________位;用四舍五入法将130.96精确到十分位是_______________;
相关试题

