【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
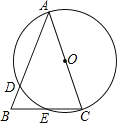
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
参考答案:
【答案】(1)见解析;(2)9
【解析】
试题分析:(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE;
(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.
(1)证明:连结AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
(2)连结DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴△BED∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BA=9,
∴AC=BA=9.

-
科目: 来源: 题型:
查看答案和解析>>【题目】同一个平面内的三条直线两两相交,最多有a个交点,最少有b个交点,则a+b=______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】设一组数据x1,x2…xn的方差为S2,将每个数据都加上2,则新数据的方差为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.

(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你写出一个有一根为1的一元二次方程: .(答案不唯一)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B点的坐标为____________;
-
科目: 来源: 题型:
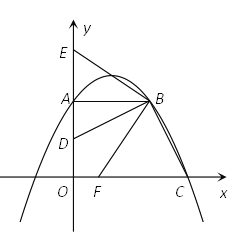
查看答案和解析>>【题目】如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连结EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
相关试题

