【题目】已知关于x的一元二次方程x2﹣2(1﹣m)x+m2=0的两实数根为x1 , x2 , 则y=x1+x2+2x1x2的最小值为 .
参考答案:
【答案】![]()
【解析】解:∵关于x的一元二次方程x2﹣2(1﹣m)x+m2=0有实数根,
∴△=[﹣2(1﹣m)]2﹣4m2=4﹣8m≥0,
∴m≤ ![]() .
.
∵关于x的一元二次方程x2﹣2(1﹣m)x+m2=0的两实数根为x1,x2,
∴x1+x2=2(1﹣m),x1x2=m2,
∴y=x1+x2+2x1x2=2(1﹣m)+2m2=2m2﹣2m+2=2(m﹣ ![]() )2+
)2+ ![]() .
.
∵m≤ ![]() ,
,
∴当m= ![]() 时,y取最小值,最小值为
时,y取最小值,最小值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解求根公式(根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根),还要掌握根与系数的关系(一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点
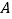 表示的数为
表示的数为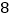 ,
,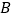 是数轴上位于点
是数轴上位于点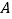 左侧一点,且AB=20,动点
左侧一点,且AB=20,动点 从
从 点出发,以每秒
点出发,以每秒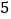 个单位长度的速度沿数轴向左匀速运动,设运动时间t(t>0)秒.
个单位长度的速度沿数轴向左匀速运动,设运动时间t(t>0)秒.
(1)写出数轴上点
 表示的数______;点
表示的数______;点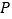 表示的数_______(用含
表示的数_______(用含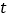 的代数式表示)
的代数式表示)(2)动点
 从点
从点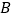 出发,以每秒
出发,以每秒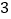 个单位长度的速度沿数轴向右匀速运动,若点
个单位长度的速度沿数轴向右匀速运动,若点 、
、 同时出发,问多少秒时
同时出发,问多少秒时 、
、 之间的距离恰好等于
之间的距离恰好等于 ?
?(3)动点
 从点
从点 出发,以每秒
出发,以每秒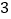 个单位长度的速度沿数轴向左匀速运动,若点
个单位长度的速度沿数轴向左匀速运动,若点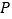 、
、 同时出发,问多少秒时
同时出发,问多少秒时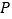 、
、 span>之间的距离恰好又等于
span>之间的距离恰好又等于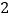 ?
?(4)若
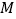 为
为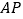 的中点,
的中点,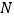 为
为 的中点,在点
的中点,在点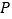 运动的过程中,线段
运动的过程中,线段 的长度是否发生变化?若变化,请说明理由,若不变,请画出图形,并求出线段
的长度是否发生变化?若变化,请说明理由,若不变,请画出图形,并求出线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
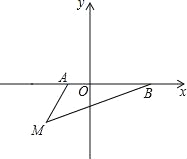
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=
 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,A(1,3),B(2,1),直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为______________________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,
中,  三个顶点坐标分别为
三个顶点坐标分别为 ,
, ,
, .
.(1)请画出
 关于
关于 轴对称的图形
轴对称的图形 ;
;(2)将
 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘 ,得到对应的点
,得到对应的点 、
、 、
、 ,请画出
,请画出
 ;
; (3)求
 与
与 的面积比,即
的面积比,即 :
: =________(不写解答过程,直接写出结果).
=________(不写解答过程,直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】穿越青海境内的兰新高速铁路正在加紧施工.某工程队承包了一段全长1957米的隧道工程,甲、乙两个班组分别从南北两端同时掘进,已知甲组比乙组每天多掘进0.5米,经过6天施工,甲、乙两组共掘进57米.
(1)求甲乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天比原来多掘进0.3米,乙组平均每天比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

相关试题

