【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB. 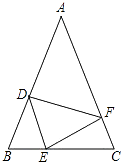
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
参考答案:
【答案】
(1)证明:∵AB=AC,
∴∠B=∠C.
∵AB=AD+BD,AB=AD+EC,
∴BD=EC.
在△DBE和△ECF中,
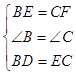 ,
,
∴△DBE≌△ECF(SAS)
∴DE=EF,
∴△DEF是等腰三角形
(2)解:∵∠A=40°,
∴∠B=∠C= ![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∴∠BDE+∠DEB=110°.
又∵△DBE≌△ECF,
∴∠BDE=∠FEC,
∴∠FEC+∠DEB=110°,
∴∠DEF=70°.
【解析】(1)通过全等三角形的判定定理SAS证得△DBE≌△ECF,由“全等三角形的对应边相等”推知DE=EF,所以△DEF是等腰三角形;(2)由等腰△ABC的性质求得∠B=∠C= ![]() (180°﹣40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等: ∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°.
(180°﹣40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等: ∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点A(m,n)在x轴上,且位于原点的左侧,则下列结论正确的是( )
A. m=0,n为一切数 B. m=0,n<0
C. m为一切数,n=0 D. m<0,n=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中:
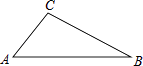
(1)用直尺和圆规,在AB上找一点D,使点D到B、C两点的距离相等(不写作法.保留作图痕迹)
(2)连接CD,已知CD=AC,∠B=25°,求∠ACB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)解分式方程: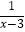 =3+
=3+ 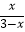
(2)解不等式组: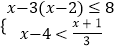 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=80°,则∠A的补角是( )
A.100°B.80°C.40°D.10°
-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节前夕,某商店根据市场调查,用1320元购进第一批盒装粽子,上市后很快售完,接着又用2880元购进第二批这种盒装粽子,已知第二批所购的粽子盒数是第一批所购粽子盒数的2倍,且每盒粽子的进价比第一批的进价多1元.
(1)第一批盒装粽子购进多少盒?
(2)若两批粽子按相同的标价销售,最后剩下50盒按八折优惠售出,如果两批粽子全部售出后利润不低于25%(不考虑其他因素),那么每盒粽子的标价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.

(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数.
相关试题

