【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)求二次函数y=ax2+bx+c的表达式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.

参考答案:
【答案】(1)y=﹣x2+4x+5;(2)点P(![]() ,
,![]() )时,S四边形APCD最大=
)时,S四边形APCD最大=![]() ;(3)当M点的坐标为(1,8)时,N点坐标为(2,13),当M点的坐标为(3,8)时,N点坐标为(2,3).
;(3)当M点的坐标为(1,8)时,N点坐标为(2,13),当M点的坐标为(3,8)时,N点坐标为(2,3).
【解析】
试题(1)设出抛物线解析式,用待定系数法求解即可;(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值;(3)先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.
试题解析:(1)设抛物线解析式为y=a![]() +9,∵抛物线与y轴交于点A(0,5), ∴4a+9=5,
+9,∵抛物线与y轴交于点A(0,5), ∴4a+9=5,
∴a=﹣1, y=﹣![]() +9=-
+9=-![]() +4x+5,
+4x+5,
(2)当y=0时,-![]() +4x+5=0,∴x1=﹣1,x2=5,∴E(﹣1,0),B(5,0),
+4x+5=0,∴x1=﹣1,x2=5,∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,∵A(0,5),B(5,0),∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;设P(x,﹣![]() +4x+5), ∴D(x,﹣x+5),
+4x+5), ∴D(x,﹣x+5),
∴PD=-![]() +4x+5+x﹣5=-
+4x+5+x﹣5=-![]() +5x, ∵AC=4, ∴S四边形APCD=
+5x, ∵AC=4, ∴S四边形APCD=![]() ×AC×PD=2(-
×AC×PD=2(-![]() +5x)=-2
+5x)=-2![]() +10x,
+10x,
∴当x=![]() 时, ∴S四边形APCD最大=
时, ∴S四边形APCD最大=![]() ,
,
(3)如图,
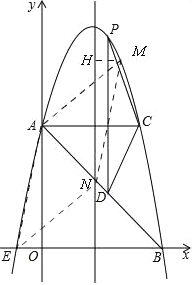
过M作MH垂直于对称轴,垂足为H,∵MN∥AE,MN=AE,∴△HMN≌△AOE,∴HM=OE=1,
∴M点的横坐标为x=3或x=1,当x=1时,M点纵坐标为8,当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),∵A(0,5),E/span>(﹣1,0), ∴直线AE解析式为y=5x+5,
∵MN∥AE,∴MN的解析式为y=5x+b,∵点N在抛物线对称轴x=2上,∴N(2,10+b),
∵AE2=OA2+0E2=26 ∵MN=AE ∴MN2=AE2, ∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8), ∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上, ∴M1N=M2N, ∴1+(b+2)2=26, ∴b=3,或b=﹣7,
∴10+b=13或10+b=3 ∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3),
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)是由抛物线y=﹣x2+x+2先作关于y轴的轴对称图形,再将所得到的图象向下平移3个单位长度得到的,点Q1(﹣2.25,q1),Q2(1.5,q2)都在抛物线y=ax2+bx+c(a≠0)上,则q1,q2的大小关系是( )
A. q1>q2 B. q1<q2 C. q1=q2 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,O为坐标原点,直线y=kx+b经过点A(﹣2,﹣1),交y轴负半轴于点B,且∠ABO=30°,过点A作直线AC⊥x轴于点C,点P在直线AC上.

(1)k= ;b= ;
(2)设△ABP的面积为S,点P的纵坐标为m.
①当m>0时,求S与m之间的函数关系式;
②当S=2时,求m的值;
③当m>0且S=4时,以BP为边作等边△BPQ,请直接写出符合条件的所有点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家八纵八横高铁网络规划中“京昆通道”的重要组成部分──西成高铁于2017年12月6日开通运营,西安至成都列车运行时间由14小时缩短为3.5小时.张明和王强相约从成都坐高铁到西安旅游.如图,张明家(记作A)在成都东站(记作B)南偏西30°的方向且相距4000米,王强家(记作C)在成都东站南偏东60°的方向且相距3000米,则张明家与王强家的距离为( )
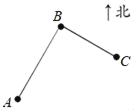
A. 6000米 B. 5000米 C. 4000米 D. 2000米
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图所示的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)64的展开式中第63项的系数为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】沿海城市A接到台风警报,在该市正南方向130km的B处有一台风中心,沿BC方向以15km/h的速度向D移动,已知城市A到BC的距离AD=50km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?

相关试题

