【题目】如图,在△ABC中,∠C=90°,CD⊥AB于D,在(1)DCAB=ACBC;(2)![]() ;(3)
;(3)![]() ;(4)AC+BC>CD+AB中正确的个数是( )
;(4)AC+BC>CD+AB中正确的个数是( )

![]()
A.4B.3C.2D.1
参考答案:
【答案】B
【解析】
(1)根据题意可以得到△ACD∽△ABC,然后用相似三角形的对应边的比相等证明其成立.
(2)用射影定理得到![]() ,
,![]() ,代入等式可以证明其成立.
,代入等式可以证明其成立.
(3)根据射影定理有:AC2=ADAB,BC2=BDAB,然后由△ACD∽△CBD,得到CD2=ADBD,代入等式可以证明其成立,
(4)根据三角形三边的关系,只能得到AC+BC>AB,不能把三角形的高代进去比较大小.
解:(1)根据直角三角形斜边上的高分直角三角形所得的两个三角形与原三角形相似,有:△ACD∽△ABC,
∴AC:AB=DC:BC,
∴DCAB=ACBC.所以(1)正确.
(2)由射影定理有:![]() ,
,![]() ,
,
∴![]() ,所以(2)正确.
,所以(2)正确.
(3)∵![]() ,
,![]() ,
,
又△ACD∽△CBD,∴![]()
![]() 所以(3)正确.
所以(3)正确.
(4)根据三角形两边之和大于第三边,只能得到AC+BC>AB,不能得到AC+BC>AB+CD.所以(4)不正确.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN//EF, 点C 为两直线之间一点,若∠CAM 的平分线与∠CBF 的平分线所在的直线相交于点 D ,则∠ACB与 ∠ADB 之间的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣
 |+(﹣1)2017+(8﹣
|+(﹣1)2017+(8﹣  )0﹣
)0﹣  +(
+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
A. 36 B. 12 C. 6 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是A1C1的中点,则AA1:BB1=_____.
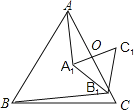
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,C为AD上一点,AB=CD=1,∠ABC=90°,∠CBD=30°,则AC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=
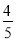 ,求AF的长.
,求AF的长.
相关试题

