【题目】如图,在△ABD中,C为AD上一点,AB=CD=1,∠ABC=90°,∠CBD=30°,则AC=_____.

参考答案:
【答案】![]()
【解析】
首先利用有30°角的直角三角形的性质和勾股定理,设BE为x,求得DE用x表示;作DE垂直于AB的延长线于点E,设AC为y,利用平行线分线段成比例,用x表示y;再利用△ABC∽△AED,求得BC(用含x的式子表示),最后在Rt△ABC中再利用勾股定理建立方程,求出x,从而解决问题.
解:分别过点A、C作AE⊥BD,CF⊥BD交BD于点,F两点,
如图所示:

设CF的长为x,AC的长为y,
∵AE⊥BD,
∴∠AEB=90°,
又∵∠ABE+∠ABC+∠CBD=180°,
∠ABC=90°,∠CBD=30°,
∴∠ABE=60°,
又∵AB=1,
∴AE=![]() ,
,
又∵CF⊥BD,
∴∠CFB=∠CFD=90°,
又∵∠CBD=30°,
∴BC=2x,
又∵∠ABC=90°,AB=1,
∴![]() ,
,
∴![]() ,
,
又∵AE⊥BD,CF⊥BD,
∴CF∥AE,
∴△DCF∽△DAE,
∴![]() ,
,
即 ,
,
整理得:![]() ,
,
两边分别平方得:![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
整理得:![]() ,
,
![]() ,
,
解得:y=﹣2(舍去),y=![]() ,
,
即AC的长为![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
A. 36 B. 12 C. 6 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,CD⊥AB于D,在(1)DCAB=ACBC;(2)
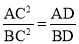 ;(3)
;(3) ;(4)AC+BC>CD+AB中正确的个数是( )
;(4)AC+BC>CD+AB中正确的个数是( )

A.4B.3C.2D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是A1C1的中点,则AA1:BB1=_____.
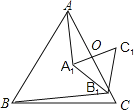
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=
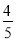 ,求AF的长.
,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
① 20.2×19.8 ;
②
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
相关试题

