Question

【题目】如图，在四边形ABCD中，AB=6，BC=8，CD=24，AD=26，∠B=90°，以AD为直径作圆O，过点D作DE∥AB交圆O于点E

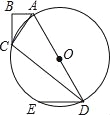
（1）证明点C在圆O上；

（2）求tan∠CDE的值；

（3）求圆心O到弦ED的距离．

Answer 1

【答案】(1)详见解析；（2）；（3）圆心O到弦ED的距离为．

【解析】

试题分析：（1）如图1，连结CO．先由勾股定理求出AC=10，再利用勾股定理的逆定理证明△ACD是直角三角形，∠C=90°，那么OC为Rt△ACD斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半得出OC=AD=r，即点C在圆O上；（2）如图2，延长BC、DE交于点F，∠BFD=90°．根据同角的余角相等得出∠CDE=∠ACB．在Rt△ABC中，利用正切函数定义求出tan∠ACB==，则tan∠CDE=tan∠ACB=；（3）如图3，连结AE，作OG⊥ED于点G，则OG∥AE，且OG=AE．易证△ABC∽△CFD，根据相似三角形对应边成比例求出CF=，那么BF=BC+CF=．再证明四边形ABFE是矩形，得出AE=BF=，所以OG=AE=．

试题解析：（1）证明：如图1，连结CO．

∵AB=6，BC=8，∠B=90°，

∴AC=10．

又∵CD=24，AD=26，102+242=262，

∴△ACD是直角三角形，∠C=90°．

∵AD为⊙O的直径，

∴AO=OD，OC为Rt△ACD斜边上的中线，

∴OC=AD=r，

∴点C在圆O上；

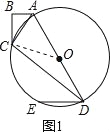
（2）解：如图2，延长BC、DE交于点F，∠BFD=90°．

∵∠BFD=90°，

∴∠CDE+∠FCD=90°，

又∵∠ACD=90°，

∴∠ACB+∠FCD=90°，

∴∠CDE=∠ACB．

在Rt△ABC中，tan∠ACB==，

∴tan∠CDE=tan∠ACB=；

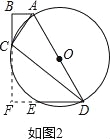
（3）解：如图3，连结AE，作OG⊥ED于点G，则OG∥AE，且OG=AE．

易证△ABC∽△CFD，

∴=，即=，

∴CF=，

∴BF=BC+CF=8+=．

∵∠B=∠F=∠AED=90°，

∴四边形ABFE是矩形，

∴AE=BF=，

∴OG=AE=，

即圆心O到弦ED的距离为．