【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A’B’C’,若它移动的距离AA’等于1cm,则两个三角形重叠部分的面积为____________cm2.
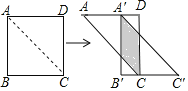
参考答案:
【答案】1
【解析】
设AC与A′B′交于点E,A′C′与DC交于点F,由正方形的性质得到△ACD和△A′B′C′都为直角边为2cm的等腰直角三角形;从而判定出△AA′E也为等腰直角三角形,得到A′E=AA′=1cm,从而得到A′D的长;由正方形的性质与三角形的面积公式即可求出两三角形重叠的面积.
对图形进行点标注,
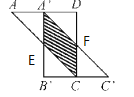
∵ 四边形ABCD是正方形边长为2cm,
∴ ∠ADC=90° ,AD=DC=2cm,∠DAC=45°,
∵△ A′ B′C′是由△ABC沿着AD方向平移得到的,
∴ AC∥A′C′,∠EA′A=90°,
∵ ∠DAC=45°,∠EA′A=90°,
∴△EAA′是等腰直角三角形,
∵AA′=1cm,△EAA′是等腰直角三角形,
∴![]()
∵ AC∥A′C′,∠DAC=45°,
∴ ∠FA′D=45°,
∵∠DA′F=45°,∠ADC=90°,
∴△FDA′是等腰直角三角形,
∵ AD=2cm,AA′=1cm,
∴A′D=1cm,
∵△FDA′是等腰直角三角形,A′D=1cm,
![]()
同理可得到![]() (cm2),
(cm2),
∴S阴影=![]() (cm2).
(cm2).
故答案为:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE.请说明EF平分∠AED.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,下列说法正确的有( )
①同一平面内,过点A有且只有一条直线AC垂直于直线l;②线段AB,AC,AD中,AC最短,根据是“两点之间的所有连线中,线段最短”;③线段AB,AC,AD中,AC最短,根据是“直线外一点,与直线上各点连接的所有线段中,垂线段最短”;④线段AC的长是点A到直线l的距离.

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( )

A.﹣4<P<0
B.﹣4<P<﹣2
C.﹣2<P<0
D.﹣1<P<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2105的坐标为_______________.
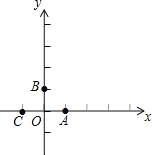
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
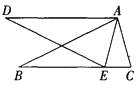
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
相关试题

