【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.

(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
参考答案:
【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)(1,0)
,0);(3)(1,0)
【解析】
试题分析:(1)由抛物线y=ax2+bx﹣4过点A(4,0)、B(﹣2,0)根据待定系数法求解即可;
(2)设点P运动到点(x,0)时,有BP2=BDBC,在![]() 中,令x=0时,则y=﹣4,即可求得点C的坐标,由PD∥AC可得△BPD∽△BAC,再根据相似三角形的性质求解即可;
中,令x=0时,则y=﹣4,即可求得点C的坐标,由PD∥AC可得△BPD∽△BAC,再根据相似三角形的性质求解即可;
(3)由△BPD∽△BAC,根据相似三角形的性质及二次函数的性质求解即可.
(1)∵抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点
∴![]() ,解得
,解得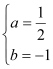
∴抛物线的解析式为![]() ;
;
(2)设点P运动到点(x,0)时,有BP2=BDBC,
在![]() 中,令x=0时,则y=﹣4
中,令x=0时,则y=﹣4
∴点C的坐标为(0,﹣4)
∵PD∥AC
∴△BPD∽△BAC
∴![]()
∵![]() ,AB=6,BP=x﹣(﹣2)=x+2
,AB=6,BP=x﹣(﹣2)=x+2
∴![]() ,即
,即![]()
∵BP2=BDBC,
∴![]() ,解得x1=
,解得x1=![]() ,x2=﹣2(不合题意,舍去)
,x2=﹣2(不合题意,舍去)
∴点P的坐标是(![]() ,0)
,0)
∴当点P运动到(![]() ,0)时,BP2=BDBC;
,0)时,BP2=BDBC;
(3)∵△BPD∽△BAC,
∴![]()
∴![]() ,
,
又∵![]() ,
,
∴![]()
∵![]() <0,∴当x=1时,S△BPC有最大值为3
<0,∴当x=1时,S△BPC有最大值为3
∴点P的坐标为(1,0)时,△PDC的面积最大。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中的点P(-4,6)在第_________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(a2)3÷a4的计算结果是( )
A.a
B.a2
C.a4
D.a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式-x>a+2的解集是x<3,则a=_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°

(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求
 的长.
的长.
相关试题

