【题目】已知:如图,矩形ABCD的对角线交于点O,DE∥AC,CE∥BD.求证:四边形OCED是菱形. 
参考答案:
【答案】证明:∵DE∥AC,即DE∥OC, CE∥BD,即CE∥OD.
∴四边形OCED是平行四边形.
又∵四边形ABCD是矩形,
∴OC= ![]() AC,OD=
AC,OD= ![]() BD,
BD,
且AC=BD,
∴OC=OD.
∴四边形OCED是菱形
【解析】先求出四边形OCED是菱形,再根据矩形的对角线互相平分且相等求出OC=OD,然后根据一组邻边相等的平行四边形是菱形证明.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4x3﹣9x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABOD的周长为4
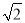 ,点P到x轴、y轴的距离与点A到x轴、y轴的距离分别相等.
,点P到x轴、y轴的距离与点A到x轴、y轴的距离分别相等.(1)请你写出正方形ABOD各顶点的坐标;
(2)求点P的坐标及三角形PDO的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

-
科目: 来源: 题型:
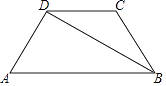
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC=2,BD平分∠ABC,∠A=60°.求:梯形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-s)7÷(-s)5 =____.
相关试题

