【题目】如图,在□ABCD 中,E、F为对角线AC上的两点,且AE=CF.

(1)求证:四边形DEBF是平行四边形;
(2)如果DE=3,EF=4,DF=5,求EB、DF两平行线之间的距离.
参考答案:
【答案】(1)详见解析;(2)2.4.
【解析】
(1)根据平行四边形的性质可得AD=BC,AD∥BC,继而可得∠DAE=∠BCF,然后即可利用SAS证明△ADF≌△CBE,进一步即可证明DF=EB,DF∥EB,即可证得结论;
(2)先根据勾股定理的逆定理得出DE⊥EF,然后根据三角形的面积即可求出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∴∠DAE=∠BCF,
∵AE=CF,∴AF=CE,
∴△ADF≌△CBE(SAS),
∴DF=EB,∠DFA=∠BEC,
∴DF∥EB,
∴四边形DEBF是平行四边形;
(2)解:∵![]() ,
,![]() ,
,
∴![]() ,∴DE⊥EF.
,∴DE⊥EF.
过点E作EG⊥DF于G,如图,则![]() ,即3×4=EG×5,∴EG=2.4.
,即3×4=EG×5,∴EG=2.4.
∴EB、DF两平行线之间的距离为2.4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,以OA为半径的圆分别交AB、AC于点E、D,在BC的延长线上取点F,使得BF=EF.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若∠A=30°,求证:DG=
 DA;
DA;(3)若∠A=30°,且图中阴影部分的面积等于2
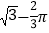 ,求⊙O的半径的长.
,求⊙O的半径的长.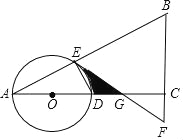
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为6,点E、F分别在BC、DC上,CE=DF=2,DE与AF相交于点G,点H为AE的中点,连接GH.
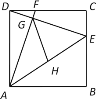
(1)求证:△ADF≌△DCE;
(2)求GH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计划建一个长方形养鸡场,为了节省材料,利用一道足够长的墙做为养鸡场的一边,另三边用铁丝网围成,如果铁丝网的长为35m.
(1)计划建养鸡场面积为150m2,则养鸡场的长和宽各为多少?
(2)能否建成的养鸡场面积为160m2?如果能,请算出养鸡场的长和宽;如果不能,请说明理由.
-
科目: 来源: 题型:
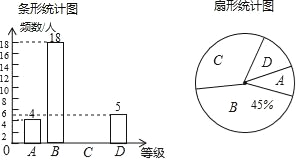
查看答案和解析>>【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
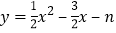 (
(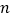 >0)与
>0)与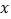 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与 轴交于点C。
轴交于点C。(1)如图1,若△ABC为直角三角形,求
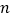 的值;
的值;(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交
 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求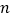 的值.
的值.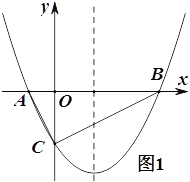
相关试题

