【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
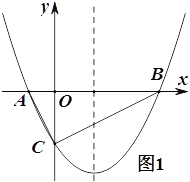
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
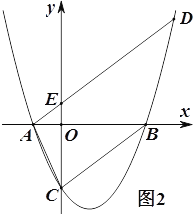
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)点P的坐标为
;(2)点P的坐标为![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用三角形相似可求AOOB,再由一元二次方程根与系数关系求AOOB构造方程求n;
(2)求出B、C坐标,设出点Q坐标,利用平行四边形对角线互相平分性质,分类讨论点P坐标,分别代入抛物线解析式,求出Q点坐标;
(3)设出点D坐标(a,b),利用相似表示OA,再由一元二次方程根与系数关系表示OB,得到点B坐标,进而找到b与a关系,代入抛物线求a、n即可.
(1)若△ABC为直角三角形
∴△AOC∽△COB
∴OC2=AOOB
当y=0时,0=![]() x2-
x2-![]() x-n
x-n
由一元二次方程根与系数关系
-OAOB=OC2
n2=![]() =2n
=2n
解得n=0(舍去)或n=2
∴抛物线解析式为y=![]() ;
;
(2)由(1)当![]() =0时
=0时
解得x1=-1,x2=4
∴OA=1,OB=4
∴B(4,0),C(0,-2)
∵抛物线对称轴为直线x=-![]() =
=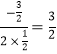
∴设点Q坐标为(![]() ,b)
,b)
由平行四边形性质可知
当BQ、CP为平行四边形对角线时,点P坐标为(![]() ,b+2)
,b+2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,则P点坐标为(
,则P点坐标为(![]() ,
,![]() )
)
当CQ、PB为为平行四边形对角线时,点P坐标为(-![]() ,b-2)
,b-2)
代入y=![]() x2-
x2-![]() x-2
x-2
解得b=![]() ,则P坐标为(-
,则P坐标为(-![]() ,
,![]() )
)
综上点P坐标为(![]() ,
,![]() ),(-
),(-![]() ,
,![]() );
);
(3)设点D坐标为(a,b)
∵AE:ED=1:4
则OE=![]() b,OA=
b,OA=![]() a
a
∵AD∥AB
∴△AEO∽△BCO
∵OC=n
∴![]()
∴OB=![]()
由一元二次方程根与系数关系得,![]()
∴b=![]() a2
a2
将点A(-![]() a,0),D(a,
a,0),D(a,![]() a2)代入y=
a2)代入y=![]() x2-
x2-![]() x-n
x-n
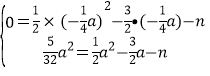
解得a=6或a=0(舍去)
则n=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD 中,E、F为对角线AC上的两点,且AE=CF.

(1)求证:四边形DEBF是平行四边形;
(2)如果DE=3,EF=4,DF=5,求EB、DF两平行线之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计划建一个长方形养鸡场,为了节省材料,利用一道足够长的墙做为养鸡场的一边,另三边用铁丝网围成,如果铁丝网的长为35m.
(1)计划建养鸡场面积为150m2,则养鸡场的长和宽各为多少?
(2)能否建成的养鸡场面积为160m2?如果能,请算出养鸡场的长和宽;如果不能,请说明理由.
-
科目: 来源: 题型:
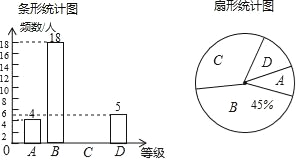
查看答案和解析>>【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图中,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6、3、2,则图中实线所围成的阴影部分面积S是( )
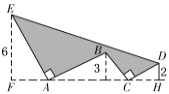
A.50B.44C.38D.32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
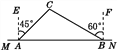
(1)MN是否穿过原始森林保护区?为什么?(参考数据:
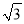 ≈1.732)
≈1.732)(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
-
科目: 来源: 题型:
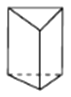
查看答案和解析>>【题目】观察下列多面体,并把下表补充完整.
名称
三棱柱
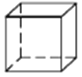
四棱柱
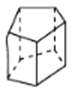
五棱柱
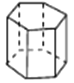
六棱柱
图形
顶点数
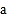
6
10
12
棱数
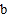
9
12
面数
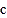
5
8
观察上表中的结果,你能发现
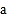 、
、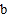 、
、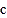 之间有什么关系吗?请写出关系式
之间有什么关系吗?请写出关系式.
相关试题

