【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
参考答案:
【答案】
(1)
证明:连接OC.
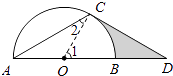
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)
解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC= ![]() .
.
在Rt△OCD中,
∵ ![]() ,
,
∴CD=2 ![]() .
.
∴ ![]() .
.
∴图中阴影部分的面积为: ![]() .
.
【解析】此题综合考查了等腰三角形的性质、切线的判定方法、扇形的面积计算方法.(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
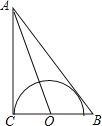
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO= ,求cosB的值.
,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC=
 ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
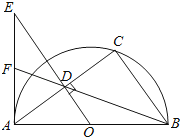
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=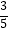 ,求AF的长.
,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣
 ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
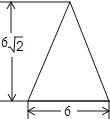
A.90°
B.120°
C.135°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
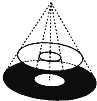
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
相关试题

