【题目】如图,在菱形ABCD中,AB=4,线段AD的垂直平分线交AC于点N,△CND的周长是10,则AC的长为 . 
参考答案:
【答案】6
【解析】解:如图, 
∵四边形ABCD是菱形,AB=4,
∴AB=CD=4,
∵MN垂直平分AD,
∴DN=AN,
∵△CND的周长是10,
∴CD+CN+DN=CD+CN+AN=CD+AC=10,
∴AC=6,
所以答案是:6.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=6,BC=8,tan∠B=
 ,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
,点D是边BC上的一个动点(点D与点B不重合),过点D作DE⊥AB,垂足为E,点F是AD的中点,连接EF,设△AEF的面积为y,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)计算:
(1)x·x7; (2)a2·a4+(a3)2;
(3)(-2ab3c2)4; (4)(-a3b)2÷(-3a5b2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(9x3y-12xy3+3xy2)÷(-3xy)-(2y+x)(2y-x),其中x=1,y=-2;
(2)(m-n)(m+n)+(m+n)2-2m2,其中m、n满足方程组
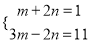
-
科目: 来源: 题型:
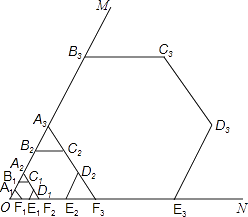
查看答案和解析>>【题目】如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1 , 边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2 , 以A2F2为边作正六边形A2B2C2D2E2F2 , 边C2D2所在的直线分别交OM、ON于点A3、F3 , 再以A3F3为边作正六边形A3B3C3D3E3F3 , …,依此规律,经第n次作图后,点Bn到ON的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF

(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两边相等的三角形的一边是7,另一边是4,则此三角形的周长是_____.
相关试题

