【题目】数轴上有两点A,B, 点C,D分别从原点O与点B出发,沿BA方向同时向左运动.
(1)如图,若点N为线段OB上一点,AB=16,ON=2,当点C,D分别运动到AO,BN的中点时,求CD的长;
(2)若点C在线段OA上运动,点D在线段OB上运动,速度分别为每秒1cm, 4cm,在点C,D运动的过程中,满足OD=4AC,若点M为直线AB上一点,且AM-BM=OM,求![]() 的值.
的值.
![]()
![]()
参考答案:
【答案】(1)9;(2)![]() 或1.
或1.
【解析】
(1)根据C,D分别为AO,BN的中点,可得ND=![]() BN,CO=
BN,CO=![]() AO,再根据CD=CO+ON+DN,将ND,CO代入可得出结果;
AO,再根据CD=CO+ON+DN,将ND,CO代入可得出结果;
(2)根据OD=4AC,BD=4CO,可得出OA:OB=1:4. 由点M为直线AB上一点,且AM-BM=OM,分两种情况求解:①当点M在线段AB上,先由已知等量关系得出AO=BM,设AO=x,再用x表示出AB,OM即可得出结果;②当点M在B点右侧时,由. AM-BM=AB=OM可得出结果.
解:(1)当点C,D分别运动到AO,BN的中点时,得
ND=![]() BN,CO=
BN,CO=![]() AO,
AO,
∴CD=CO+ON+DN=![]() AO+ON+
AO+ON+![]() BN=
BN=![]() (AO+BN)+ON=
(AO+BN)+ON=![]() (AB-ON)+ON,
(AB-ON)+ON,
又AB=16,ON=2,
∴CD=![]() ×(16-2)+2=9.
×(16-2)+2=9.
(2)∵C,D两点运动的速度比为1:4,∴BD=4CO.
又OD=4AC,∴BD+OD=4(CO+AC),
∴OB=4OA,即OA:OB=1:4.
若点M为直线AB上一点,且AM-BM=OM,
①点M在线段AB上时,如图,
![]()
∵AM-BM=OM,∴AO+OM-BM=OM,
∴AO=BM,
设AO=x,则BM=x,
由OA:OB=1:4,得BO=4x,AB=5x
∴OM=BO-BM=3x,
∴![]() .
.
②当点M在B点右侧时,如图,
![]()
∵AM-BM=OM,
∴AB=OM,
∴![]()
综上所述:![]() 的值为
的值为![]() 或1.
或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级学生参加研学活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)求该校此次参加研学活动的学生有多少人?
(2)若单独租用60座的客车,需租_______辆;
(3)已知45座客车的日租金为每辆1 000元,60座客车的日租金为每辆1 200元,该校单独租用哪种车更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰△ABC三个顶点在⊙O上,直径AB=12,P为弧BC上任意一点(不与B,C重合),直线CP交AB延长线与点Q,2∠PAB+∠PDA=90°,下列结论:①若∠PAB=30°,则弧BP的长为
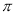 ;②若PD//BC,则AP平分∠CAB;③若PB=BD,则
;②若PD//BC,则AP平分∠CAB;③若PB=BD,则 ,④无论点P在弧
,④无论点P在弧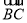 上的位置如何变化,CP·CQ为定值. 正确的是___________.
上的位置如何变化,CP·CQ为定值. 正确的是___________.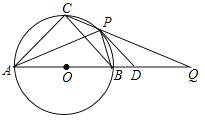
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在纸面所在的平面内,一只电子蚂蚁从数轴上表示原点的位置O点出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移动到
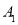 ,第2次移动到
,第2次移动到 ,第3次移动到
,第3次移动到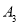 ,……,第n次移动到
,……,第n次移动到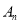 ,则△O
,则△O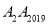 的面积是( )
的面积是( )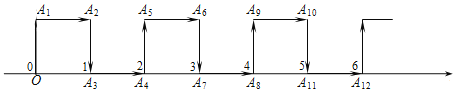
A.504B.
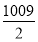 C.
C.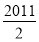 D.505
D.505 -
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车一天下午以车站为出发地在东西方向的大街上营运,规定向东为正,向西为负,行车里程(单位:
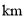 )依先后次序记录如下:
)依先后次序记录如下: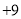 ,
, ,
,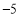 ,
,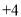 ,
,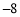 ,
,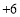 ,
, ,
,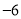 ,
,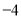 ,+10.
,+10.(1)将最后一名乘客送到目的地,出租车离车站出发点多远?在车站的什么方向?
(2)出租车在行驶过程中,离车站最远的距离是多少?
(3)出租车按物价部门规定,起步价(不超过
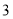 千米)为
千米)为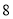 元,超过3千米的部分每千米的价格为
元,超过3千米的部分每千米的价格为 元,司机一个下午的营业额是多少?
元,司机一个下午的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在去年底以每件80元的进价购进一批同型号的服装,一月份以每件150元的售价销售了320件,二、三月份该服装畅销,销量持续走高,在售价不变的情况下,三月底统计知三月份的销量达到了500件.
(1)求二、三月份服装销售量的平均月增长率;
(2)从四月份起商场因换季清仓采用降价促销的方式,经调查发现,在三月份销量的基础上,该服装售价每降价5元,月销售量增加10件,当每件降价多少元时,四月份可获利12000元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法中不正确的是( )

A. ∠1与∠AOB是同一个角B. ∠AOC也可以用∠O表示
C. ∠β=∠BOCD. 图中有三个角
相关试题

