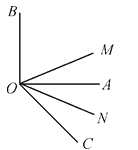
【题目】如图,∠AOB是直角,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)当∠AOC=40°,求出∠MON的大小,并写出解答过程理由;
(2)当∠AOC=50°,求出∠MON的大小,并写出解答过程理由;
(3)当锐角∠AOC=α时,求出∠MON的大小,并写出解答过程理由.
参考答案:
【答案】(1)45°;(2)45°;(3)45°.
【解析】试题分析:(1)根据∠AOB是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM是∠BOC的平分线,ON是∠AOC的平分线,即可求得答案.
(2)方法同(1);
(3)根据∠MON=∠MOC-∠NOC,又利用∠AOB是直角,可得∠MON=![]() ∠AOB=45°.
∠AOB=45°.
试题解析:(1)∵∠AOB是直角,∠AOC=40°,
∴∠AOB+∠AOC=90°+40°=130°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,
∴∠MOC=![]() ∠BOC=65°,∠NOC=
∠BOC=65°,∠NOC=![]() ∠AOC=20°.
∠AOC=20°.
∴∠MON=∠MOC-∠NOC=65°-20°=45°,
(2)∵∠AOB是直角,∠AOC=50°,
∴∠AOB+∠AOC=90°+50°=140°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,
∴∠MOC=![]() ∠BOC=70°,∠NOC=
∠BOC=70°,∠NOC=![]() ∠AOC=25°.
∠AOC=25°.
∴∠MON=∠MOC-∠NOC=70°-25°=45°;
(3)∵∠AOB=90°,∠AOC=α,
∴∠AOB+∠AOC=∠BOC=90°+α.
∵OM平分∠BOC,
∴∠MOC=![]() ∠BOC=45°+
∠BOC=45°+![]() α.
α.
∵ON是∠AOC的角平分线,
∴∠1=![]() ∠AOC=
∠AOC=![]() α.
α.
∴∠MOC-∠1=45°+![]() α-
α-![]() α=45°.
α=45°.
即∠MON=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形.
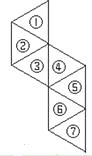
(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
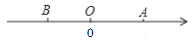
查看答案和解析>>【题目】如图,已知数轴上点B表示的为-5,点A是数轴上一点,且AB=12,动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点H从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
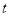 (
(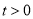 )秒.
)秒.(1)写出数轴上点A表示的数 ;
(2)当动点P,H同时从点A和点B出发,运动
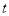 秒时,点P表示的数 ;点H表示的数 ;(用含
秒时,点P表示的数 ;点H表示的数 ;(用含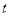 的代数式表示)
的代数式表示)(3)动点P、H同时出发,问点H运动多少秒时追上点P?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD为正方形, E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G。

(1)求证:DE+BG=EG;∠EAG=45°;
(2)AB=1,GF=m,FE=n,求m+n+mn的值;
(3)若AB=6,∠BAG=∠CEG,求GE. -
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为-4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t大于0)秒.
(1)点C表示的数为__________;
(2)当点P运动到达点A处时运动时间t为秒__________;
(3)运动过程中点P表示的数的表达式为_____________;(用含字母t的式子表示)
(4)当t等于多少秒时,P、C之间的距离为2个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在各地区基本普及使用,某市一商场为响应号召,推广销售,该商场计划用3800元购进两种节能灯共120只,这两种节能灯的进价、售价如下表:

(1)求甲、乙两种型号节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利多少元?
相关试题

