【题目】已知:如图,四边形ABCD为正方形, E为CD边上的一点,连接AE,并以AE为对称轴,作与△ADE成轴对称的图形△AFE,延长EF(或FE)交直线BC于G。
(1)求证:DE+BG=EG;∠EAG=45°;
(2)AB=1,GF=m,FE=n,求m+n+mn的值;
(3)若AB=6,∠BAG=∠CEG,求GE.
参考答案:
【答案】
(1)
解:∵以AE为对称轴,作与△ADE成轴对称的图形△AFE,
∴△ADE≌△AFE,
∴AD=AF=AB,DE=FE,∠DAE=∠FAE,∠D=∠AFE=∠AFG=90°=∠B,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠EAG=∠FAE+∠FAG= ![]() ∠BAD=45°,
∠BAD=45°,
∴GE=GF+EF=BG+DE.
(2)
解:∵AB=1,GF=m,FE=n,则EG=m+n,CG=1-m,CE=1-n,
∵∠C=90°,
∴(1-m)2+(1-n)2=(m+n)2,
整理得:m+n+mn=1.
(3)
解:由(1)可得Rt△ABG≌Rt△AFG,
∴∠BGA=∠FGA.
∵∠BAG=∠CEG,
∴∠BGA=∠CGE,
∴∠BGA=∠CGE=∠FGA= ![]() .
.
则∠BAG=∠CEG=30°,
∴BG= ![]() AB=2
AB=2 ![]() ,
,
∴CG=AB-BG=6-2 ![]() ,
,
∴GE=2CG=12-4 ![]() .
.
【解析】(1)根据HL,Rt△ABG≌Rt△AFG,根据全等三角形的性质,及等量代换可解答;(2)在Rt△CEG中,由勾股定理可得CG2+CE2=EG2 , 将入相应的m,n的代数式,即可求得;(3)易证得到∠BGA=∠CGE=∠FGA= ![]() .则∠BAG=∠CEG=30°,再根据含30°角的直角三角形的三边关系,求出相应边的长度.
.则∠BAG=∠CEG=30°,再根据含30°角的直角三角形的三边关系,求出相应边的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上,七个边长为1的等边三角形,分别用①至⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形.
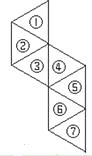
(1)你取出的是哪个三角形?写出平移的方向和平移的距离;
(2)将取出的三角形任意放置在拼成的正六边形所在平面,问:正六边形没有被三角形盖住的面积能否等于 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点B表示的为-5,点A是数轴上一点,且AB=12,动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,动点H从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
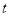 (
(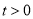 )秒.
)秒.(1)写出数轴上点A表示的数 ;
(2)当动点P,H同时从点A和点B出发,运动
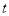 秒时,点P表示的数 ;点H表示的数 ;(用含
秒时,点P表示的数 ;点H表示的数 ;(用含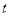 的代数式表示)
的代数式表示)(3)动点P、H同时出发,问点H运动多少秒时追上点P?
-
科目: 来源: 题型:
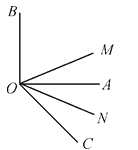
查看答案和解析>>【题目】如图,∠AOB是直角,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)当∠AOC=40°,求出∠MON的大小,并写出解答过程理由;
(2)当∠AOC=50°,求出∠MON的大小,并写出解答过程理由;
(3)当锐角∠AOC=α时,求出∠MON的大小,并写出解答过程理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为cm2 .
-
科目: 来源: 题型:
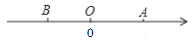
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为-4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t大于0)秒.
(1)点C表示的数为__________;
(2)当点P运动到达点A处时运动时间t为秒__________;
(3)运动过程中点P表示的数的表达式为_____________;(用含字母t的式子表示)
(4)当t等于多少秒时,P、C之间的距离为2个单位长度.

相关试题

