【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2 ![]() ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 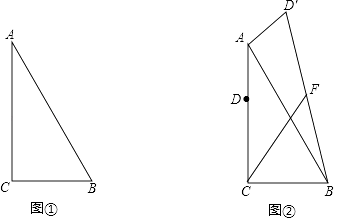
参考答案:
【答案】6;180;![]()
【解析】解:(Ⅰ)如下图①所示: 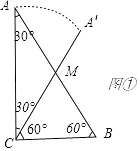
∵将线段CA绕点C顺时针旋转30°,
∴△AMC 为等腰三角形,AM=MC
∵∠BAC=30°,
∴△MBC为等边三角形,
∴AM=MB=CM
又∵BC=6,
∴AB=2BC=12,
∴CM=6
所以答案是:6
(Ⅱ)∵在RtABC中,∠ACB=90°,BAC=30°,BC=6,
∴AC= ![]() BC=6
BC=6 ![]()
当将线段AD绕点A逆时针旋转 180度时,线段CF的长最大,如图②所示: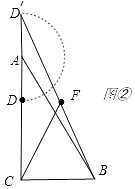
∵AD=AD′,
∴CD′=8 ![]() ,
,
∵在RtABC中,∠ACB=90°,BC=6,
∴BD′= ![]() =
= ![]() =2
=2 ![]()
∵点F是BD′的中点,
∴CF= ![]() BD′=
BD′= ![]()
即:当将线段AD绕点A逆时针旋转 180度时,线段CF的长最大,最大值为 ![]()
所以答案是:180; ![]()
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并在括号内加注理由。
如图,已知
 ∥
∥ ,
, 、
、 分别平分
分别平分 和
和

求证:

证明:∵
 ∥
∥
∴
 = ( )
= ( ) ∵
 、
、 平分
平分 、
、
∴
 =
=
∴
 =
= ( )
( )∴
 =
=
∴ ∥ ( )
∴
 =∠ ( )
=∠ ( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于F,连接BD交CE于G,AE和BD交于点H,则下列结论:①AE=DB;②不另外添加线,图中全等三角形只有1对;③若连接FG,则△CFG是等边三角形;④若连接CH,则CH平分∠FHG.其中正确的是________(填序号).
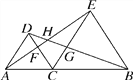
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:三角形
 中,
中,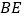 、
、 分别是
分别是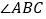 和
和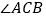 的平分线,
的平分线,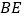 、
、 相交于点
相交于点 (知识链接:三角形三个内角的和是180°。如图
(知识链接:三角形三个内角的和是180°。如图 是三角形
是三角形 的一个内角)
的一个内角)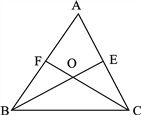
(1)如果
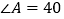 °求
°求 的度数。
的度数。(2)如果
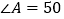 °直接写出
°直接写出 的度数
的度数(3)探求
 和
和 的关系(用等式表示),并简要说明理由。
的关系(用等式表示),并简要说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
相关试题

