【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.

参考答案:
【答案】(1)见解析;(2)AE=1.
【解析】(1)欲证明AE=BF,只要证明△DEA≌△DFB即可.
(2)根据CE=CF,设AE=BF=x,列出方程即可.
(1)如图,连接AD、BD.
∵∠DCE=∠DCB,DE⊥CA,DF⊥CB,∴DE=DF,∠AED=∠DFB=90°.
∵DG垂直平分AB,∴DA=DB.
在Rt△DEA和Rt△DFB中,![]() ,
,
∴△DEA≌△DFB,∴AE=BF.
(2)设AE=BF=x.在Rt△CDE和Rt△CDF中,![]() ,
,
∴△CDE≌△CDF,∴CE=CF,∴6+x=8﹣x,∴x=1,∴AE=1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2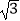 ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 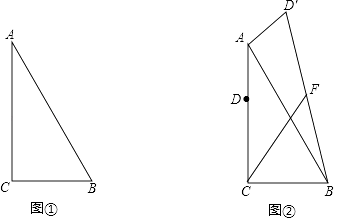
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:三角形
 中,
中,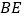 、
、 分别是
分别是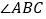 和
和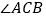 的平分线,
的平分线,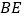 、
、 相交于点
相交于点 (知识链接:三角形三个内角的和是180°。如图
(知识链接:三角形三个内角的和是180°。如图 是三角形
是三角形 的一个内角)
的一个内角)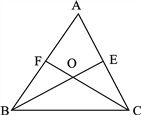
(1)如果
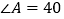 °求
°求 的度数。
的度数。(2)如果
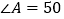 °直接写出
°直接写出 的度数
的度数(3)探求
 和
和 的关系(用等式表示),并简要说明理由。
的关系(用等式表示),并简要说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=m2
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).

(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
相关试题

