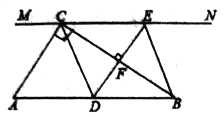
【题目】如图:在Rt△ABC中,∠ACB=90°,过点C的直线MN//AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE.
(1)求点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由.
(2)在(1)的条件下,当∠A= 时,四边形BECD是正方形.说明你的理由.
参考答案:
【答案】(1)平行四边形BECD是菱形,理由见解析;(2)45°
【解析】
(1)先证明AC∥DE,得出四边形BECD是平行四边形,再“根据直角三角形斜边上的中线等于斜边的一半”证出CD=BD,得出四边形BECD是菱形;
(2)先求出∠ABC=45°,再根据菱形的性质求出∠DBE=90°,即可证出结论.
(1)当点D是AB的中点时,四边形BECD是菱形;理由如下:
∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
∵D为AB中点,
∴AD=BD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=![]() AB=BD,
AB=BD,
∴四边形BECD是菱形;
(2)当∠A=45°时,四边形BECD是正方形;理由如下:
∵∠ACB=90°,∠A=45°,
∴∠ABC=45°,
∵四边形BECD是菱形,
∴∠ABC=![]() ∠DBE,
∠DBE,
∴∠DBE=90°,
∴四边形BECD是正方形.
故答案为:45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与y轴交于点
与y轴交于点 ,与x轴交于点
,与x轴交于点 ,点B坐标为
,点B坐标为 .
. 求二次函数解析式及顶点坐标;
求二次函数解析式及顶点坐标; 过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点
过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点 点P在AC上方
点P在AC上方 ,作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
,作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1) -11-7-8+6 (2)(-0.6)+1.7+(+0.6)+(-1.7 )-9
(3)
 (4)
(4)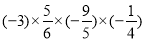
(5)
 (6)
(6)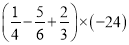
-
科目: 来源: 题型:
查看答案和解析>>【题目】彩虹服装店用
 元购进
元购进 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, (单位:元).他卖完这
(单位:元).他卖完这 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱? -
科目: 来源: 题型:
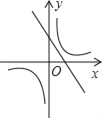
查看答案和解析>>【题目】如图,已知关于x的函数y=k(x﹣1)和
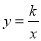 (k≠0),它们在同一坐标系内的图象大致是( )
(k≠0),它们在同一坐标系内的图象大致是( )A.
 B.
B. 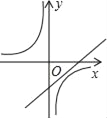 C.
C. 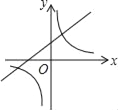 D.
D. 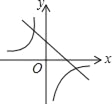
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把顺次连接四边形各边中点所得的四边形叫做中点四边形.若一个任意四边形的面积为a,则它的中点四边形面积为( )
A.
 aB.
aB.  C.
C. D.
D.
-
科目: 来源: 题型:
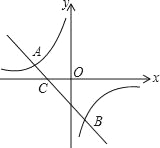
查看答案和解析>>【题目】如图,已知A(﹣4,2),B(n,﹣4)是一次函数y=kx+b的图象与反比例函数
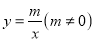 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的表达式;
(2)根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围.
相关试题

