【题目】如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
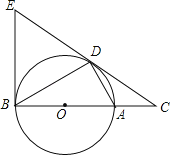
(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
参考答案:
【答案】(1)证明见解析(2)5
【解析】
试题分析:(1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=![]() ,易证Rt△CDO∽Rt△CBE,得到
,易证Rt△CDO∽Rt△CBE,得到![]() ,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=![]() ,
,
∴tan∠OEB=![]() =
=![]() ,
,
∵Rt△CDO∽Rt△CBE,(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
∴![]()
![]() ,
,
∴CD=![]() ×12=8,
×12=8,
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,
解得x=5.
即BE的长为5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A=∠B+∠C,则对△ABC的形状判断正确的是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:﹣3(x﹣2y)+4(x﹣2y)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,再回答问题:
要比较代数式A、B的大小,可以作差A-B,比较差的取值,当A-B>0时,有A>B;当A-B=0时,有A=B;当A-B<0时,有A<B.”例如,当a<0时,比较
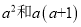 的大小.可以观察
的大小.可以观察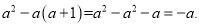 因为当a<0时,-a>0,所以当a<0时,
因为当a<0时,-a>0,所以当a<0时,  .
.
(1)已知M=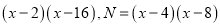 ,比较M、N的大小关系.
,比较M、N的大小关系.(2)某种产品的原料提价,因而厂家决定对于产品进行提价,现有三种方案:
方案1:第一次提价p%,第二次提价q%;
方案2:第一次提价q%,第二次提价p%;
方案3:第一、二次提价均为

如果设原价为a元,请用含a、p、q的式子表示提价后三种方案的价格.
方案1: ;方案2: ;方案3:_______
如果p,q是不相等的正数,三种方案哪种提价最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
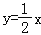 与双曲线
与双曲线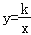 (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线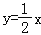 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线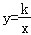 (k>0,x>0)交于点B.
(k>0,x>0)交于点B.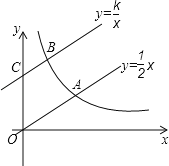
(1)设点B的横坐标分别为b,试用只含有字母b的代数式表示k;
(2)若OA=3BC,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上离开原点4个长度单位的点表示的数是 ________ 。
相关试题

