【题目】甲、乙两人共同解方程组![]() , 由于甲看错了方程①中的a,得到方程组的解为
, 由于甲看错了方程①中的a,得到方程组的解为![]() ;乙看错了方程②中的b,得到方程组的解为
;乙看错了方程②中的b,得到方程组的解为![]() , 试计算a2012+(
, 试计算a2012+(![]() b)2013的值.
b)2013的值.
参考答案:
【答案】解:∵甲看错了方程①中的a,得到方程组的解为![]() ,
,
∴﹣12+b=﹣2,
解得:b=10,
∵乙看错了方程②中的b,得到方程组的解为![]() ,
,
∴5a+20=15,
解得:a=﹣1,
则a2012+(![]() b)2013=
b)2013=![]() =1+(﹣1)=0.
=1+(﹣1)=0.
【解析】根据方程组的解的定义,![]() 应满足方程②,
应满足方程②,![]() 应满足方程①,将它们分别代入方程②①,就可得到关于a,b的二元一次方程组,解得a,b的值,即可解答.
应满足方程①,将它们分别代入方程②①,就可得到关于a,b的二元一次方程组,解得a,b的值,即可解答.
【考点精析】认真审题,首先需要了解二元一次方程的解(适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为BC的中点,F是CD上一点,且∠AEF=90°,求证:CF=
 AB.
AB. 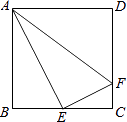
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批零件共有3000件,为了检查这批零件的质量,从中随机抽取一部分测量了它们的长度(单位:mm),并根据得到的数据,绘制出如下的统计图①和图②.
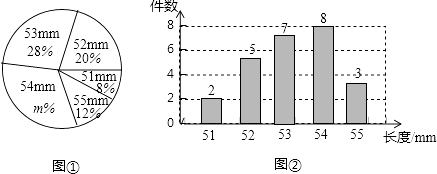
(1)本次随机抽取的零件的件数为 , 图①中m的值为;
(2)求本次随机抽取的零件长度的平均数、中位数和众数;
(3)根据样本数据,估计该批零件中长度为52mm的零件件数. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)a24÷[(a2) 3) 4;
(2)( a3·a4) 2÷(a3) 2÷a;
(3)- x12÷(-x4) 3;
(4)( x6÷x4·x2) 2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程x2﹣8x+3=0配方成如下的形式,则正确是( )
A.(x+4)2=13
B.(x﹣4)2=19
C.(x﹣4)2=13
D.(x+4)2=19 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别是2和6,第三边长为偶数,则这个三角形的周长是 ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若□×2xy=16x3y2 , 则□内应填的单项式是( )
A.4x2y
B.8x3y2
C.4x2y2
D.8x2y
相关试题

