搜索
【题目】如图，在△ABC中，∠ACB=90°，点D，E分别在AC，BC上，且∠CDE=∠B，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．若AC=8，AB=10，则CD的长为 ．
参考答案：
【答案】
．
【解析】
试题分析：由折叠可得，∠DCE=∠DFE=90°，∴D，C，E，F四点共圆，∴∠CDE=∠CFE=∠B，又∵CE=FE，∴∠CFE=∠FCE，∴∠B=∠FCE，∴CF=BF，同理可得，CF=AF，∴AF=BF，即F是AB的中点，∴Rt△ABC中，CF=
AB=5，由D，C，E，F四点共圆，可得∠DFC=∠DEC，由∠CDE=∠B，可得∠DEC=∠A，∴∠DFC=∠A，又∵∠DCF=∠FCA，∴△CDF∽△CFA，∴CF2=CD×CA，即52=CD×8，∴CD=，故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算(a4)2的结果为( )
A.a8B.a6C.a2D.a16
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组数中，不是勾股数的是（ ）
A. 0.3，0.4，0.5 B. 5，12，13 C. 10， 24，26 D. 7，24，25
-
科目： 来源： 题型：
查看答案和解析>>【题目】小慧根据学习函数的经验，对函数
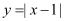的图象与性质进行了研究，下面是小慧的研究过程，请补充完成：
⑴函数
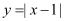的自变量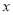
的取值范围是 ；⑵列表，找出
与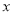
的几组对应值.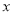
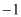
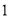
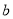
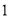
其中，
；⑶在平面直角坐标系
中，描出以上表中各队对应值为坐标的点，并画出该函数的图象；⑷写出该函数的一条性质： .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数
的图象经过点D，四边形BCFG的面积为8，则k的值为（ ）
A.16
B.20
C.24
D.28 -
科目： 来源： 题型：
查看答案和解析>>【题目】菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=
，BD=2，则菱形ABCD的面积为 ． 
-
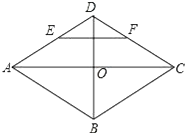
科目： 来源： 题型：
查看答案和解析>>【题目】为了“创建文明城市，建设美丽家园”，我市某社区将辖区内的一块面积为1000m2的空地进行绿化，一部分种草，剩余部分栽花，设种草部分的面积为x（m2），种草所需费用
（元）与x（m2）的函数关系式为
，其图象如图所示：栽花所需费用
（元）与x（m2）的函数关系式为
（0≤x≤1000）．（1）请直接写出
、
和b的值；（2）设这块1000m2空地的绿化总费用为W（元），请利用W与x的函数关系式，求出绿化总费用W的最大值；
（3）若种草部分的面积不少于700m2，栽花部分的面积不少于100m2，请求出绿化总费用W的最小值．
相关试题
