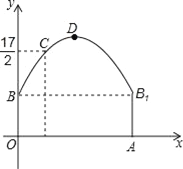
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
参考答案:
【答案】(1)拱顶D到地面OA的距离为10m;(2)这辆货车能安全通过;(3)两排灯的水平距离最小是4![]() m.
m.
【解析】试题分析:(1)先确定B点和C点坐标,然后利用待定系数法求出抛物线解析式,再利用配方法确定顶点D的坐标,从而得到点D到地面OA的距离;
(2)由于抛物线的对称轴为直线x=6,而隧道内设双向行车道,车宽为4m,则货运汽车最外侧与地面OA的交点为(2,0)或(10,0),然后计算自变量为2或10的函数值,再把函数值与6进行大小比较即可判断;
(3)抛物线开口向下,函数值越大,对称点之间的距离越小,于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值.
解:(1)根据题意得B(0,4),C(3,![]() ),
),
把B(0,4),C(3,![]() )代入y=﹣
)代入y=﹣![]() x2+bx+c得
x2+bx+c得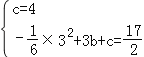 ,
,
解得![]() .
.
所以抛物线解析式为y=﹣![]() x2+2x+4,
x2+2x+4,
则y=﹣![]() (x﹣6)2+10,
(x﹣6)2+10,
所以D(6,10),
所以拱顶D到地面OA的距离为10m;
(2)由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=![]() >6,
>6,
所以这辆货车能安全通过;
(3)令y=8,则﹣![]() (x﹣6)2+10=8,解得x1=6+2
(x﹣6)2+10=8,解得x1=6+2![]() ,x2=6﹣2
,x2=6﹣2![]() ,
,
则x1﹣x2=4![]() ,
,
所以两排灯的水平距离最小是4![]() m.
m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,BD为对角线,点P从A出发,沿射线AB运动,连接PD,过点D作DE⊥PD,交直线BC于点E.

(1)当点P在线段AB上时(如图1),求证:BP+CE=
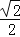 BD;
BD; (2)当点P在线段AB的延长线上时(如图2),猜想线段BP、CE、BD之间满足的关系式,并加以证明;
(3)若直线PE分别交直线BD、CD于点M、N,PM=3,EN=4,求PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣
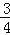 x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣ x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣ x+3于点Q,则当PQ=BQ时,a的值是 .
x+3于点Q,则当PQ=BQ时,a的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,5)所在的象限是( ).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=2m+1和x=2n﹣1时,多项式x2+4x+8的值相等,且m﹣n+1≠0,则当x=m+n时,多项式x2+4x+8的值= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本﹣1,0,2,x,3,它们的平均数是2,则x=_____,方差S2=_____。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等式2a□a=2a2一定成立,则□内的运算符号为( )
A.+ B.﹣ C.× D.÷
相关试题

