【题目】如图,大楼AB高16m,远处有一塔CD,某人在楼底B处测得塔顶C的仰角为39°,在楼顶A处测得塔顶的仰角为22°,求塔高CD的高.(结果保留小数后一位)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,si39°≈0.63,cos39°≈0.78,tan39°≈0.81.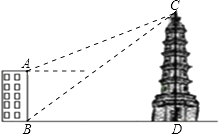
参考答案:
【答案】解:过点A作AE⊥CD于点E,
由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米
设大楼与塔之间的距离BD的长为x米,则AE=BD=x米,
∵在Rt△BCD中,tan∠CBD= ![]() ,
,
∴CD=BD tan 39°≈0.81x,
∵在Rt△ACE中,tan∠CAE= ![]() ,
,
∴CE=AE×tan 22°≈0.4x,
∵CD﹣CE=DE,
∴0.81x﹣0.4x=16,
解得x≈39.0,
即BD=39.0(米),
∴CD=0.81×39.0=31.6(米),
答:塔高CD是31.6米.
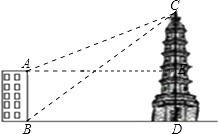
【解析】过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=39°,ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用x表示出CD和CE=AE,利用CD﹣CE=DE得到有关x的方程,求得x的值即可.
【考点精析】根据题目的已知条件,利用关于仰角俯角问题的相关知识可以得到问题的答案,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.
求证:(1)BC=AD;
(2)△OAB是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】公园门票价格规定如下:

某校七年级(1)(2)两个班共104人去游园,其中(1)班有40多人,且不足50人,经估算,如果两个班都以班为单位进行购票,则一共应付1240元,问:
(1)两个班各有多少个学生?
(2)如果两班联合起来,作为一个团体票能省多少钱?如果七(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数的图象,一定经过原点的是( )
A.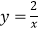
B.y=5x2﹣3x
C.y=x2﹣1
D.y=﹣3x+7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),
 为直线
为直线 上点,过点
上点,过点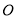 作射线
作射线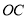 ,
,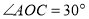 ,将一直角三角尺(
,将一直角三角尺(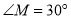 )的直角顶点放在点
)的直角顶点放在点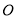 处,一边
处,一边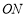 在射线
在射线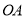 上,另一边
上,另一边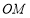 与
与 都在直线
都在直线 的上方.
的上方.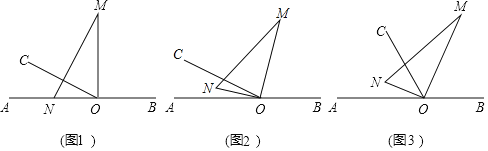
(1)若将图(1)中的三角尺绕点
 以每秒
以每秒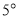 的速度,沿顺时针方向旋转
的速度,沿顺时针方向旋转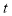 秒,当
秒,当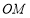 恰好平分
恰好平分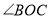 时,如图(2).
时,如图(2).①求
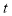 值;
值;②试说明此时
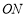 平分
平分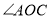 ;
;(2)将图(1)中的三角尺绕点
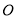 顺时针旋转,设
顺时针旋转,设 ,
,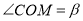 , 当
, 当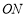 在
在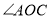 内部时,试求
内部时,试求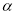 与
与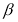 的数量关系;
的数量关系;(3)若将图(1)中的三角尺绕点
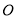 以每秒
以每秒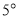 的速度沿顺时针方向旋转的同时,射线
的速度沿顺时针方向旋转的同时,射线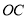 也绕点
也绕点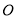 以每秒
以每秒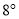 的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线
的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线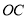 第一次平分
第一次平分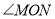 ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点A(-2,1)、B(-3,4),C(-5,2)均在格点上.在所给直角坐标系中解答下列问题:
(1)将△ABC平移得到△A1B1C1,使得点B的对应点B1与原点O重合,在所给直角坐标系中画出图形;
(2)在图中画出△ABC关于y轴对称的△A2B2C2;
(3)在x轴上找一点P,使得△PAB2的周长最小,请直接写出点P的坐标.

相关试题

