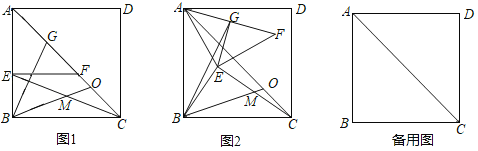
【题目】在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.
(1)如图1,E在边AB上时,![]() = ,∠GBM= ;
= ,∠GBM= ;
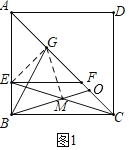
(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否任然成立?请加以证明.
(3)若BE=2,则CO长为 .
参考答案:
【答案】(1)![]() ,45°;(2)成立,理由见解析;(3)
,45°;(2)成立,理由见解析;(3)![]() 或3
或3![]() .
.
【解析】
(1)连结EG、GM.想办法证明△GBM是等腰直角三角形即可解决问题.
(2)成立.延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.利用全等三角形的性质证明△GBM是等腰直角三角形即可解决问题.
(3)分两种情形①点E在线段AB上.②点E在AB的延长线上,分别求解即可解决问题.
解:(1)连结EG、GM.
∵四边形ABCD是正方形,
∴∠ABC=90°,∠CAB=∠ACB=45°,
∵EF⊥AB,
∴∠AEF=90°,
∴∠EAF=∠EFA=45°,
∵AG=GF,
∴EG⊥AF,
∴∠EGC=90°
∵EM=MC,
∴GM=BM=![]() CE,
CE,
∴∠MCG=∠MGC,∠MBC=∠MCB,
∴∠BMG=∠BME+∠GME=2∠BMC+2∠GCM=2∠ACB=90°.
故△GMB为等腰直角三角形.
∴![]() .
.
故答案为![]() ,45°.
,45°.
(2)成立.
理由:延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.
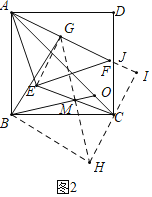
∵EM=MC,GM=MH,∠EMG=∠HMC,
∴△EMG≌△CMH(SAS),
∴EG=CH,∠EGM=∠MHC,
∴EC∥CH,
∴∠AGE=∠AIH=90°,
∵AG=EG,
∴AG=CH,
∵∠D=∠I=90°,∠AJD=∠CJI,
∴∠ICD=∠IAD,
∵∠BAG+∠IAD=90°,∠BCH+∠ICF=90°
∴∠BCH=∠BAG,
∵BA=BC
∴△BAG≌△BCH(SAS),
∴BG=DH,∠ABG=∠CBH,
∴∠∠GBH=∠ABC=90°
故△GBH是等腰直角三角形,
∴![]() ,∠GBM=45°.
,∠GBM=45°.
(3)当E在B上方时,如图3﹣1中,延长BO交CD于T.
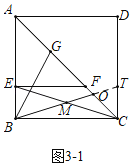
∴BE∥CT,
∴∠MEB=∠MCT,
∵∠EMB=∠CMT,EM=CM,
∴△EMB≌△CMT(ASA),
∴BE=CT=2,
∵CT∥AB,
∴![]() ,
,
∵AC=6![]() ,
,
∴OC=![]() ×6
×6![]()
∴CO=![]()
当E在B下方时同法可得CO=3![]() .
.
综上所述,OC的长为![]() 或3
或3![]() .
.
故答案为![]() 或3
或3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣
 ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y与x的函数解析式;
(2)每分进水、出水各多少升?
(3)第 分钟时该容器内的水恰好为10升.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+8分别交两轴于点A、B,点C的横坐标为4,点D在线段OA上,且AD=7.
(1)求直线CD的解析式;
(2)P为直线CD上一点,若△PAB面积为20,求P的坐标;
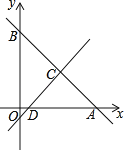
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC 上的点,∠1=∠2,∠C=∠D
求证: DF∥AC

证明:∵ ∠1=∠2(已知),∠1=∠3 ,∠2=∠4( ),
∴ ∠3=∠4( ),
∴ ∥__________( ).
∴ ∠C=∠ABD( ).
∵ ∠C=∠D( ),
∴ ∠D =__________( ).
∴ DF∥AC( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=ax+b交x轴于点A,交y轴于点B,且a,b满足a=
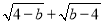 +4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.
+4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.(1)a= ,b= ,C坐标为 ;
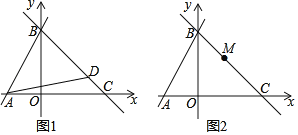
(2)如图1,k=﹣1时,求点D的坐标;
(3)如图2,在(2)的条件下,点M是直线y=kx﹣4k上一点,连接AM,将AM绕A顺时针旋转90°得AQ,OQ最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(2m-3)x+m+2.
(1)若函数图像过原点,求m的值;
(2)若函数图像过点(-1,0),求m的值;
(3)若函数图像平行于直线y=-x+2求m的值;
(4)若函数图像经过第一、二、四象限,求m的取值范围.
相关试题

