【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y与x的函数解析式;
(2)每分进水、出水各多少升?
(3)第 分钟时该容器内的水恰好为10升.

参考答案:
【答案】(1)y=![]() x+15(4≤x≤12);(2)每分进水的速度为5(L/min);出水管的出水速度是每分钟
x+15(4≤x≤12);(2)每分进水的速度为5(L/min);出水管的出水速度是每分钟![]() (L/min);(3)2或
(L/min);(3)2或![]() .
.
【解析】
(1)利用待定系数法解答即可;
(2)根据图象列式计算即可;
(3)根据题意列方程解答即可.
(1)设当4≤x≤12时,求y与x的函数解析式为y=kx+b,根据题意得![]() ,解得
,解得
![]() ,
,
∴y=![]() x+15(4≤x≤12);
x+15(4≤x≤12);
(2)每分进水的速度为:50÷4=5(L/min);
出水管的出水速度是每分钟5-![]() =
=![]() (L/min);
(L/min);
(3)设t分钟时该容器内的水恰好为10升,根据题意得,
5t=10或![]() (t12)=3010,
(t12)=3010,
解得t=2或![]() .
.
故答案为:2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知点A(0,10),点P(m,10),连接AP、OP,将△AOP沿直线OP翻折得到△EOP(点A的对应点为点E).若点E到x轴的距离不大于6,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣
 ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+8分别交两轴于点A、B,点C的横坐标为4,点D在线段OA上,且AD=7.
(1)求直线CD的解析式;
(2)P为直线CD上一点,若△PAB面积为20,求P的坐标;
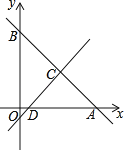
-
科目: 来源: 题型:
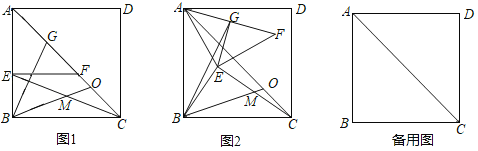
查看答案和解析>>【题目】在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.
(1)如图1,E在边AB上时,
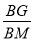 = ,∠GBM= ;
= ,∠GBM= ;(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否任然成立?请加以证明.
(3)若BE=2,则CO长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC 上的点,∠1=∠2,∠C=∠D
求证: DF∥AC

证明:∵ ∠1=∠2(已知),∠1=∠3 ,∠2=∠4( ),
∴ ∠3=∠4( ),
∴ ∥__________( ).
∴ ∠C=∠ABD( ).
∵ ∠C=∠D( ),
∴ ∠D =__________( ).
∴ DF∥AC( ).
相关试题

