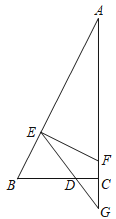
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)请探究线段AF与FG的倍数关系,并证明你的结论。
(3)设FG=x,△EFG的面积为y,求y关于x的函数解析式,并直接写出x的取值范围;
参考答案:
【答案】(1)见解析;(2)AF=3 FG ;(3)![]()
【解析】分析:(1)先证明∠A=∠2,然后利用相似三角形的判定方法即可得到结论;
(2)证明△EFG∽△AEG即可得解.
(3)作EH⊥AF于点H,如图1,利用勾股定理计算出AB=2![]() ,利用△EFG∽△AEG得到
,利用△EFG∽△AEG得到![]() ,再证明Rt△AEF∽Rt△ACB得到
,再证明Rt△AEF∽Rt△ACB得到![]() ,所以
,所以![]() ,则EG=2x,AG=4x,AF=3x,EF=
,则EG=2x,AG=4x,AF=3x,EF=![]() x,AE=
x,AE=![]() x,接着利用相似比表示出EH=
x,接着利用相似比表示出EH=![]() x,AH=
x,AH=![]() x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
x,然后根据三角形面积公式表示出y与x的关系,最后利用CF=4-3x可确定x的范围;
详解:(1)证明:∵ED=BD,
∴∠B=∠2,
∵∠ACB=90°,
∴∠B+∠A=90°.
∵EF⊥AB,
∴∠BEF=90°,
∴∠1+∠2=90°,
∴∠A=∠2,
∵∠EGF=∠AGE,
∴△EFG∽△AEG;
(2)答:AF=3 FG
证明:作EH⊥AF于点H.
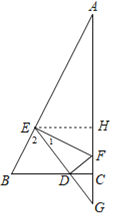
∵ 在Rt△ABC中,∠ACB=90°,BC=2,AC=4,
∴ ![]() .
.
∴ 在Rt△AEF中,∠AEF=90°,![]() .
.
∵ △EFG∽△AEG,
∴ ![]() .
.
∴ EG=2 FG,
∴AG=2 EG=4 FG
∴AF=3 FG
(3)∵ FG=x,
∴ EG=2x,AG=4x.
∴ AF=3x.
∵ EH⊥AF,
∴ ∠AHE=∠EHF=90°.
∴ ∠EFA+∠FEH=90°.
∵ ∠AEF=90°,
∴ ∠A+∠EFA=90°.
∴ ∠A=∠FEH.
∴ tanA =tan∠FEH.
∴ 在Rt△EHF中,∠EHF=90°,![]() .
.
∴ EH=2HF.
∵ 在Rt△AEH中,∠AHE=90°,![]() .
.
∴ AH=2EH.
∴ AH=4HF.
∴ AF=5HF.
∴ HF=![]() .
.
∴ ![]() .
.
∴ ![]() .
.
x的取值范围![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】粮库6天内粮食进出库的吨数如下(“+”表示进库“-”表示出库)
+25, +8,-12,+34,-36,-22.
(1)经过这6天,粮库里的粮食是增多还是减少了?通过计算说明.
(2)经过这6天,仓库管理员结算发现库里还存480吨粮,那么6天前库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A-B=7a2-7ab,且B=-4a2+5ab+8.(1)求A等于多少?
(2)若 ,求A的值.
,求A的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
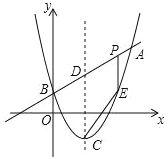
(1)求m的值和该二次函数的表达式.为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(3)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形纸片ABCD中,AB=2,BC=3.
操作:将矩形纸片沿EF折叠,使点B落在边CD上.
探究:(1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由;
(2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比;
(3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中,众数和中位数分别是( )
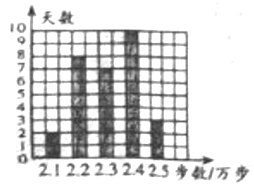
A. 2.2,2.3B. 2.4,2.3C. 2.4,2.35D. 2.3,2.3
相关试题

