【题目】探究:
(1)如图①,在等腰直角三角形ABC中,∠ACB=90,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE
填空:
①线段BD、BE的数量关系为______.
②线段BC、DE的位置关系为______.
推广:
(2)如图②,在等腰三角形ABC中,顶角∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE请判断(1)中的结论是否成立,并说明理由.
应用:
(3)如图③,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,请直接写出DE的值.

参考答案:
【答案】(1)①BD=CE;②BD⊥CE;(2)结论:(1)中的结论仍然成立,理由见解析;(3)满足条件的DE的值为![]() 或4
或4![]() .
.
【解析】
①由CA=CB,∠ACB=90°,CM平分∠ACB,得出∠ECF=∠DCF=45°,易证△CBD≌△CBE,即可得出BD=BE;
②由CD=CE即可得出BC⊥DE.
(2)由CA=CB,∠ACB=α,CM平分∠ACB,得出∠ECF=∠DCF=![]() α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
(3)分两种情况,根据三角形全等的性质及三角函数即可得出.
(1)如图①中,
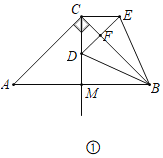
∵CA=CB,∠ACB=90°,CM平分∠ACB,
∴∠ACM=∠BCM=45°,
∵∠ECD=90°,
∴∠ECF=∠DCF=45°,
∵CD=CE,CB=CB,
∴△CBD≌△CBE(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
故答案为BD=CE,BD⊥CE.
(2)结论:(1)中的结论仍然成立.
理由:如图②中,
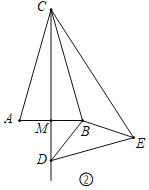
∵CA=CB,∠ACB=α,CM平分∠ACB,
∴∠ACM=∠BCM=![]() α,
α,
∵∠ECD=α,
∴∠ECF=∠DCF=![]() α,
α,
∵CD=CE,CB=CB,
∴△CBD≌△CBF(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
(3)如图③中,
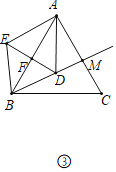
当△AFE≌△AMD时,AF=AM,
∵∠AFD=∠AMD=90°,
∵AD=AD,
∴Rt△ADF≌Rt△ADM(HL),
∴∠DAF=∠DAM=30°,
∴∠DBA=∠DAB=30°,
∴DA=DB,
∵DF⊥AB,
∴∠BDF=60°,BF=AF=2,
∵BD=BE,
∴△BDE是等边三角形,
∴DF=EF=BFtan30°=![]() ,
,
∴DE=2EF=![]() .
.
如图③-1中,当点D在AM的延长线时,易证AF=AM=2,DE=2DF=4![]() .
.
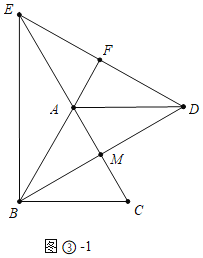
综上所述,满足条件的DE的值为![]() 或4
或4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从
 ,
, 两地相向而行,他们距
两地相向而行,他们距 地的距离
地的距离 与时间
与时间 的关系如图所示,下列说法错误的是( )
的关系如图所示,下列说法错误的是( )
A.甲的速度是
 B.甲出发4.5小时后与乙相遇
B.甲出发4.5小时后与乙相遇C.乙比甲晚出发2小时D.乙的速度是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,DE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,回答下列问题:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3-1|=2;
在数轴上,有理数5与-2对应的两点之间的距离为|5-(-2)|=7;
在数轴上,有理数-2与3对应的两点之间的距离为|-2-3|=5;
在数轴上,有理数-8与-5对应的两点之间的距离为|-8-(-5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a-b|或|b-a|,记为|AB|=|a-b|=|b-a|.

(1)数轴上有理数-10与-5对应的两点之间的距离等于______;数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为______;若数轴上有理数x与-1对应的两点A,B之间的距离|AB|=2,则x等于______;
(2)如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为-2,动点P表示的数为x.

①若点P在点M,N之间,则|x+2|+|x-4|=______;
若|x+2|+|x-4|═10,则x=______;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x-2|+|x-4|的最小值等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2018次运动后,动点P的坐标是( )

A. (2018,1)B. (2018,0)C. (2018,2)D. (2017,0)
-
科目: 来源: 题型:
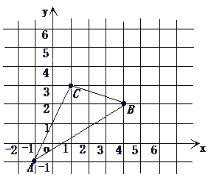
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将推理过程填写完整
如图,EF∥AD,∠1 =∠2,∠BAC = 70°。求∠AGD的度数。
解:因为EF∥AD(已知)
所以 ∠2 = (两直线平行,同位角相等)
又因为 ∠1 = ∠2(已知)
所以 ∠1 = ∠3(等量代换)
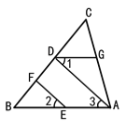
所以AB∥ ( )
所以∠BAC + = 180°( )
又因为∠BAC = 70°(已知)
所以∠AGD =
相关试题

