搜索
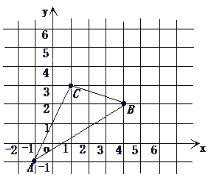
【题目】如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标.
（2）求出△ABC的面积.
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化位置。
参考答案：
【答案】（1）A（-1，-1），B（4,2），C（1,3）（2）7（3）见解析
【解析】
(1)观察各点在坐标系中的位置，写出坐标即可；
(2)利用三角形ABC所在的长方形的面积减去四周的三个三角形的面积即可；
(3)根据平行的性质找到各点的对应点，顺次连接即可.
(1)由图可知，A(-1，-1)，B(4，2)，C(1，3)；
(2)S△ABC=4×5-
×2×4-×1×3-×3×5=20-4-
-
=7；
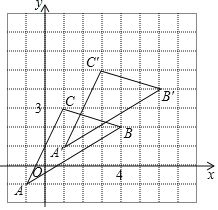
(3)如图，△A′B′C′即为所求．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料，回答下列问题：
数轴是学习有理数的一种重要工具，任何有理数都可以用数轴上的点表示，这样能够运用数形结合的方法解决一些问题．例如，两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示；
在数轴上，有理数3与1对应的两点之间的距离为|3-1|=2；
在数轴上，有理数5与-2对应的两点之间的距离为|5-(-2)|=7；
在数轴上，有理数-2与3对应的两点之间的距离为|-2-3|=5；
在数轴上，有理数-8与-5对应的两点之间的距离为|-8-(-5)|=3；……
如图1，在数轴上有理数a对应的点为点A，有理数b对应的点为点B，A，B两点之间的距离表示为|a-b|或|b-a|，记为|AB|=|a-b|=|b-a|．
(1)数轴上有理数-10与-5对应的两点之间的距离等于______；数轴上有理数x与-5对应的两点之间的距离用含x的式子表示为______；若数轴上有理数x与-1对应的两点A，B之间的距离|AB|=2，则x等于______；
(2)如图2，点M，N，P是数轴上的三点，点M表示的数为4，点N表示的数为-2，动点P表示的数为x．
①若点P在点M，N之间，则|x+2|+|x-4|=______；
若|x+2|+|x-4|═10，则x=______；
②根据阅读材料及上述各题的解答方法，|x+2|+|x|+|x-2|+|x-4|的最小值等于______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：
(1)如图①，在等腰直角三角形ABC中，∠ACB=90，作CM平分∠ACB交AB于点M，点D为射线CM上一点，以点C为旋转中心将线段CD逆时针旋转90°得到线段CE，连接DE交射线CB于点F，连接BD、BE
填空：
①线段BD、BE的数量关系为______．
②线段BC、DE的位置关系为______．
推广：
(2)如图②，在等腰三角形ABC中，顶角∠ACB=a，作CM平分∠ACB交AB于点M，点D为△ABC外部射线CM上一点，以点C为旋转中心将线段CD逆时针旋转α度得到线段CE，连接DE、BD、BE请判断(1)中的结论是否成立，并说明理由．
应用：
(3)如图③，在等边三角形ABC中，AB=4．作BM平分∠ABC交AC于点M，点D为射线BM上一点，以点B为旋转中心将线段BD逆时针旋转60°得到线段BE，连接DE交射线BA于点F，连接AD、AE．当以A、D、M为顶点的三角形与△AEF全等时，请直接写出DE的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第2018次运动后，动点P的坐标是（ ）
A. （2018，1）B. （2018，0）C. （2018，2）D. （2017，0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】将推理过程填写完整
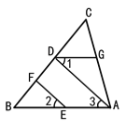
如图，EF∥AD，∠1 =∠2，∠BAC = 70°。求∠AGD的度数。
解：因为EF∥AD（已知）
所以 ∠2 = （两直线平行，同位角相等）
又因为 ∠1 = ∠2（已知）
所以 ∠1 = ∠3（等量代换）
所以AB∥ （ ）
所以∠BAC + = 180°（ ）
又因为∠BAC = 70°（已知）
所以∠AGD =
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．
平均分（分）
中位数（分）
众数（分）
方差（
）初中部
a
85
b
高中部
85
c
100
160
（1）根据图示计算出a、b、c的值；
（2）结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？
（3）计算初中代表队决赛成绩的方差
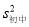，并判断哪一个代表队选手成绩较为稳定．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某批发市场经销龟苓膏粉，其中
品牌的批发价是每包20元，
品牌的批发价是每包25元，小明计划购买这两种品牌的龟苓膏粉共1000包，解答下列问题：（1）若购买这些龟苓膏粉共花费22000元，求两种品牌的龟苓膏粉各购买了多少包？
（2）若凭会员卡在此批发市场购买商品可以获得8折优惠，会员卡费用为500元，
若购买会员卡并用此卡购买这些龟苓膏粉共花费
元，设品牌购买了
包，请求出与之间的函数关系式.
相关试题
