【题目】如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?

参考答案:
【答案】乙船航行的方向为南偏东55°.
【解析】试题分析:
由题意可知:在△ABC中,AC=60,AB=80,BC=100,由此可由“勾股定理逆定理”证得∠BAC=90°,结合∠EAD=180°和∠EAC=35°即可求得∠DAB的度数,从而得到乙船的航行方向.
试题解析:
由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某校营养午餐的检测,得到如下信息:每份营养午餐的总质量
 ;午餐的成分
;午餐的成分为蛋白质、碳水化合物、脂肪和矿物质,其组成成分所占比例如图
 所示;其中矿物质的含量是脂
所示;其中矿物质的含量是脂肪含量的
 倍,蛋白质和碳水化合物含量占
倍,蛋白质和碳水化合物含量占 .
.
(
 )设其中蛋白质含量是
)设其中蛋白质含量是 .脂肪含量是
.脂肪含量是 ,请用含
,请用含 或
或 的代数式分别表示碳水化合物和矿物
的代数式分别表示碳水化合物和矿物质的质量.
(
 )求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
)求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.(
 )参考图
)参考图 ,请在图
,请在图 中完成这四种不同成分所占百分比的扇形统计图.
中完成这四种不同成分所占百分比的扇形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足:
 ,点D为x正半轴上一动点
,点D为x正半轴上一动点 (1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

-
科目: 来源: 题型:
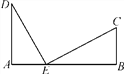
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )

A. ①②③
B. ①②④
C. ②③④
D. ①②③④
-
科目: 来源: 题型:
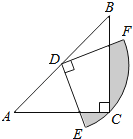
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A.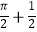
B.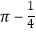
C.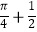
D.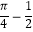
-
科目: 来源: 题型:
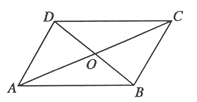
查看答案和解析>>【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.
相关试题

