【题目】已知：如图，Rt△ABC中，∠BAC=90°.

（1）按要求作图：（保留作图痕迹）

①延长BC到点D，使CD=BC；

②延长CA到点E，使AE=2CA；

③连接AD，BE并猜想线段AD与BE的大小关系；

（2）证明（1）中你对线段AD与BE大小关系的猜想.

解：（1）AD与BE的大小关系是________________.

（2）证明：

参考答案：

【答案】（1）AD=BE ；（2）详见解析.

【解析】试题分析：（1）根据基本作图，作一条线段等于已知线段的作图方法就可以作出图形；

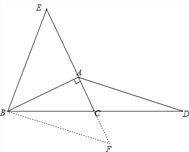
（2）延长AC到点F，使CF=AF，连接BF，证明△ACD≌△FCB，就有AD=FB，进而得出AE=AF，就可以得出BE=BF，从而结论AD=BE．

试题解析：（1）由题意，得作图如下：

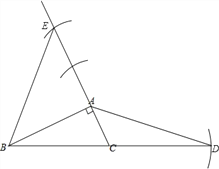
（2）延长AC到点F，使CF=AF，连接BF，

在△ACD和△FCB中，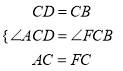

∴△ACD≌△FCB(SAS)

∴AD=FB.

∵CF=AC，

∴AF=2AC.

∵AE=2CA，

∴AF=AE，

∵∠BAC=90°，

∴AB⊥EF，

∴AB是EF的垂直平分线，

∴BE=BF，

∴AD=BE.

关闭