【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
参考答案:
【答案】
(1)证明:∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,
在△ABE和△ACF中
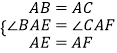 ,
,
∴△ABE≌△ACF,
∴BE=CF;

(2)解:∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF= ![]() AF=2
AF=2 ![]() ,
,
∴CD=CF﹣DF=2 ![]() ﹣2.
﹣2.
【解析】(1)根据旋转的性质得AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“SAS”证明△ABE≌△ACF,于是根据全等三角形的性质即可得到结论;(2)根据菱形的性质得DF=AF=2,DF∥AB,再利用平行线的性质得∠1=∠BAC=45°,则可判断△ACF为等腰直角三角形,所以CF= ![]() AF=2
AF=2 ![]() ,然后计算CF﹣DF即可.
,然后计算CF﹣DF即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后
 的顶点均在格点上。
的顶点均在格点上。(1)写出点
 的坐标
的坐标(2)画出
 向上平移3个单位,向左平移5个单位得到的
向上平移3个单位,向左平移5个单位得到的 的图像 ,并写出顶点坐标;
的图像 ,并写出顶点坐标;(3)求
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费
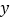 (元)与用水量
(元)与用水量 (吨)的函数关系如图所示。
(吨)的函数关系如图所示。(1)分别写出当
 和
和 时,
时,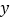 与
与 的函数关系式;
的函数关系式;(2)若某用户该月用水21吨,则应交水费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】画出函数
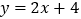 的图象,利用图象求解下列问题:
的图象,利用图象求解下列问题:(1)求方程
 的解;
的解;(2)求不等式
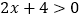 的解集;
的解集;(3)若
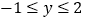 ,求
,求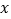 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
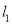 的解析表达式为
的解析表达式为 ,且
,且 与
与 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 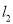 交于点
交于点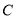 .
.
(1)求点
 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得 与
与 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成。为了种植“花海”,需要从甲乙两地向大圩A.B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A.B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
运费(元/吨)
A
B
甲地
12
12
乙地
10
8
(1)设甲地运往
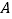 棚营养土
棚营养土 吨,请用关于
吨,请用关于 的代数式完成下表;
的代数式完成下表;运往A.B两地的吨数
A
B
甲地

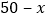
乙地
___
___
(2)设甲地运往A棚营养土
 吨,求总运费
吨,求总运费 (元)关于
(元)关于 (吨)的函数关系式(要求写出自变量取值范围).
(吨)的函数关系式(要求写出自变量取值范围).(3)当甲、乙两地各运往A.B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
-
科目: 来源: 题型:
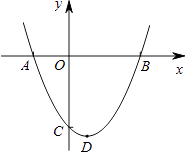
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣
 )
)
(1)求抛物线对应的函数关系式;
(2)求四边形ACDB的面积;
(3)若平移(1)中的抛物线,使平移后的抛物线与坐标轴仅有两个交点,请直接写出一个平移后的抛物线的关系式.
相关试题

