【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求出根的判别式,再根据非负数的性质即可证明;
(2)根据一元二次方程根与系数的关系即可求得方程两根的和与两根的积,两根的平方和可以用两根的和与两根的积表示,根据方程的两个实数根的平方和等于26,即可得到一个关于m的方程,求得m的值.
试题解析:(1)证明:∵关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0的判别式△=(m﹣3)2+4m(2m﹣3)=9(m﹣1)2≥0,∴无论m为何值方程都有两个实数根;
(2)解:设方程的两个实数根为x1、x2,则x1+x2=﹣(m﹣3),x1×x2=﹣m(2m﹣3),令x12+x22=26,得:(x1+x2)2﹣2x1x2=(m﹣3)2+2m(2m﹣3)=26,整理得:5m2﹣12m﹣17=0,解这个方程得:m= ![]() 或m=﹣1,所以存在正数m=
或m=﹣1,所以存在正数m= ![]() ,使得方程的两个实数根的平方和等于26.
,使得方程的两个实数根的平方和等于26.
-
科目: 来源: 题型:
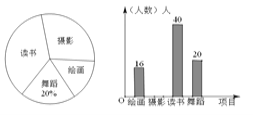
查看答案和解析>>【题目】某学校为了丰富学生业余生活,决定组建绘画、摄影、读书和舞蹈兴趣活动小组,为了解学生最喜欢哪一种活动的人数,随机抽取了部分学生进行调查(每位学生必选且只能选一项),并将调查结果绘制成了两幅不完整的统计图,请你根据统计图上提供的信息回答下列问题:
(1)这次被调查的学生共有多少人,并将条形统计图补充完整;
(2)在扇形统计图中,求出最喜欢“读书”所对应的圆心角度数;
(3)若该校共有学生2000人,请你估计该校最喜欢读书活动的人数.
-
科目: 来源: 题型:
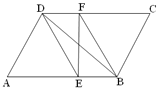
查看答案和解析>>【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小芳去商店购买甲、乙两种商品. 现有如下信息:
信息1:甲、乙两种商品的进货单价之和是5元,按零售单价购买甲商品3件和乙商品2件,共付了19元;
信息2:甲商品零售单价比甲进货单价多1元,乙商品零售单价比乙进货单价的2倍少1元.
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)若小芳准备用不超过400元钱购买100件甲、乙两种商品,其中甲种商品至少购买多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,弦AD⊥BC垂足为H,∠ABC=2∠CAD.
(1)如图1,求证:AB=BC;
(2)如图2,过点B作BM⊥CD垂足为M,BM交⊙O于E,连接AE、HM,求证:AE∥HM;
(3)如图3,在(2)的条件下,连接BD交AE于N,AE与BC交于点F,若NH=2
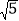 ,AD=11,求线段AB的长.
,AD=11,求线段AB的长.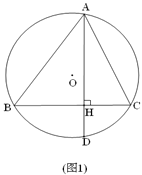
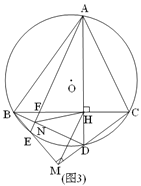

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣
(n为常数,n≠0)的图象与一次函数y=kx+8(k为常数,k≠0)的图象在第三象限内相交于点D(﹣ ,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO=
,m),一次函数y=kx+8与x轴、y轴分别相交于A、B两点.已知cos∠ABO= .
.(1)求反比例函数的解析式;
(2)点P是x轴上的动点,当△APC的面积是△BDO的面积的2倍时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,
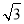 ≈1.73
≈1.73(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
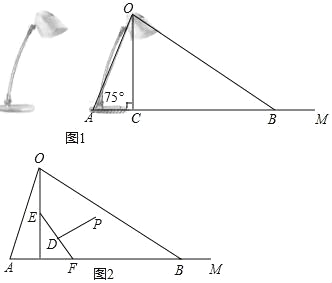
相关试题

