【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 均为格点.
均为格点.
(1)线段![]() 的长度等于______;
的长度等于______;
(2)若![]() 为线段
为线段![]() 上的动点,以
上的动点,以![]() 、
、![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形,当
为平行四边形,当![]() 长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
参考答案:
【答案】5 取格点![]() 、
、![]() 、
、![]() ,连结
,连结![]() 与
与![]() 垂直交于点
垂直交于点![]() ,延长
,延长![]() 与AB的平行线
与AB的平行线![]() 交于点Q,四边形
交于点Q,四边形![]() 即为所求
即为所求
【解析】
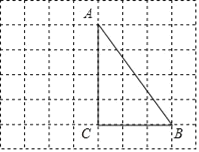
(1)根据勾股定理即可求得AB的长;
(2)取AC的中点D,过点D作DE⊥AB于点P,过点C作直线CF∥AB,交PD的延长线于点Q,连接AQ、CP,即可画出平行四边形PAQC.
(1)根据网格可知:
线段![]() 的长度为
的长度为![]() ,
,
所以线段AB的长度等于5.
故答案为5;
(2)如图所示:四边形PAQC即为所求.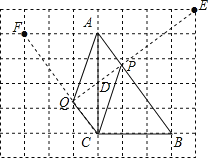
①取AC的中点D,取格点E,使DE⊥AB于点P,
②取格点F,使CF∥AB,交PD的延长线于点Q,
③连接AQ、CP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系内,
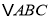 的三个顶点的分别为
的三个顶点的分别为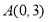 ,
,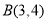 ,
,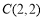 (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).
(1)在网格内画出
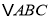 向下平移2个单位长度得到的
向下平移2个单位长度得到的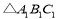 ,点
,点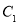 的坐标是________;
的坐标是________;(2)以点
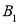 为位似中心,在网格内画出
为位似中心,在网格内画出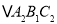 ,使
,使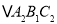 与
与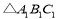 位似,且位似比为
位似,且位似比为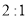 ,点
,点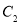 的坐标是________;
的坐标是________;(3)
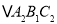 的面积是________平方单位.
的面积是________平方单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
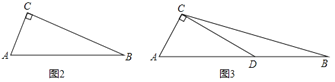
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
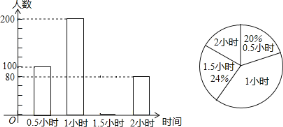
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的直径
的直径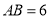 ,
,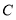 为圆周上一点,
为圆周上一点,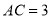 ,过点
,过点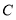 作
作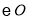 的切线
的切线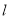 ,过点
,过点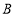 作
作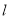 的垂线
的垂线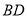 ,垂足为
,垂足为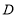 ,
,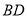 与
与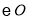 交于点
交于点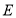 .
.(1)求
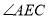 的度数;
的度数;(2)求证:四边形
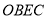 是菱形.
是菱形.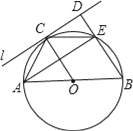
-
科目: 来源: 题型:
查看答案和解析>>【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

相关试题

