【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
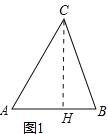
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
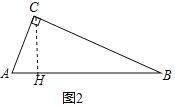
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
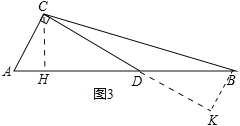
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

参考答案:
【答案】(1)2 ;(2)△ABC的面积=39;(3)T(BC,CD)=![]()
【解析】
(1)如图1,过C作CH⊥AB,根据正投影的定义求出BH的长即可;
(2)如图2,过点C作CH⊥AB于H,由正投影的定义可知AH=4,BH=9,再根据相似三角形的性质求出CH的长即可解决问题;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,求出CD、DK即可得答案.
(1)如图1,过C作CH⊥AB,垂足为H,
∵T(AC,AB)=3,
∴AH=3,
∵AB=5,
∴BH=AB-AH=2,
∴T(BC,AB)=BH=2,
故答案为:2;
(2)如图2,过点C作CH⊥AB于H,
则∠AHC=∠CHB=90°,
∴∠B+∠HCB=90°,
∵∠ACB=90°,
∴∠B+∠A=90°
∴∠A=∠HCB,
∴△ACH∽△CBH,
∴CH:BH=AH:CH,
∴CH2=AH·BH,
∵T(AC,AB)=4,T(BC,AB)=9,
∴AH=4,BH=9,
∴AB=AH+BH=13,CH=6,
∴S△ABC=(AB·CH)÷2=13×6÷2=39;
(3)如图3,过C作CH⊥AB于H,过B作BK⊥CD于K,
∵∠ACD=90°,T(AD,AC)=2,
∴AC=2,
∵∠A=60°,
∴∠ADC=∠BDK=30°,
∴CD=AC·tan60°=2![]() ,AD=2AC=4,AH=
,AD=2AC=4,AH=![]() AC=1,
AC=1,
∴DH=4-1=3,
∵T(BC,AB)=6,CH⊥AB,
∴BH=6,
∴DB=BH-DH=3,
在Rt△BDK中,∠K=90°,BD=3,∠BDK=30°,
∴DK=BD·cos30°=![]() ,
,
∴T(BC,CD)=CK=CD+DK=![]() +
+![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+4与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且△ABC面积为10.
(1)求点C的坐标及直线BC的解析式;
(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG右侧作长形FGQP,且FG:GQ=1:2,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐标;
(3)如图2,若M为线段BC上一点,且满足S△AMB=S△AOB,点E为直线AM上一动点,在x轴上是存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系内,
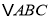 的三个顶点的分别为
的三个顶点的分别为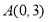 ,
,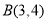 ,
,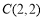 (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).
(1)在网格内画出
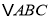 向下平移2个单位长度得到的
向下平移2个单位长度得到的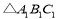 ,点
,点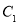 的坐标是________;
的坐标是________;(2)以点
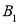 为位似中心,在网格内画出
为位似中心,在网格内画出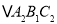 ,使
,使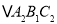 与
与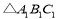 位似,且位似比为
位似,且位似比为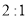 ,点
,点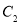 的坐标是________;
的坐标是________;(3)
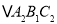 的面积是________平方单位.
的面积是________平方单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点
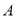 、
、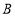 、
、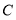 均为格点.
均为格点.(1)线段
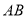 的长度等于______;
的长度等于______;(2)若
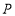 为线段
为线段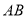 上的动点,以
上的动点,以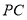 、
、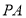 为邻边的四边形
为邻边的四边形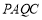 为平行四边形,当
为平行四边形,当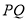 长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
长度最小时,请你借助网格和无刻度的直尺画出该平行四边形,并简要说明你的作图方法:__________(不要求证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
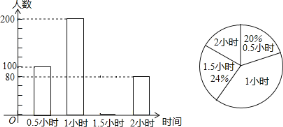
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
相关试题

