【题目】已知⊙O的直径20，OP长为8，则过P的弦中，弦长为整数的弦共有（ ）条．

A.1 B.9 C.17 D.16

参考答案：

【答案】D

【解析】

试题分析：求出过P点的弦的长度的取值范围，取特殊解，根据对称性综合求解．

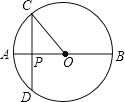
解：如图，AB是直径，OA=10，OP=8，过点P作CD⊥AB，交圆于点C，D两点．

由垂径定理知，点P是CD的中点，

∴PC=4，

在直角三角形OPC中，由勾股定理求得，PC=6，

∴CD=12，则CD是过点P最短的弦长为12；AB是过P最长的弦，长为20．

故过点P的弦的长度都在12～20之间；

因此弦长为12，13，14，15，16，17，18，19，20；

当弦长为12、20时，过P点的弦分别为弦CD和过P点的直径，分别有一条；

当弦长为13，14，15，16，17，18，19时，根据圆的对称性知，符合条件的弦应该有两条；

故弦长为整数的弦共有16条．

故选D．

关闭