【题目】如图1,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)如图2,直线BO与⊙O交于点D,E,若BD=4,AB=16,求AE的长.

参考答案:
【答案】(1)答案见解析;(2)AE=![]() .
.
【解析】试题分析:(1)连接OC,证明OC⊥AB即可;
(2)连接OC,过E作EF⊥AB与F.设⊙O的半径的半径为r,则OC=OD=r,OB=4+r.
由勾股定理可求出半径r,OC,BO,BE的长.再由△OCB∽△EFB,求出EF,BF,AF的长,从而得到结论.
试题解析:(1)证明:连接OC.

∵OA=OB,CA=CB,∴OC⊥AB.
∵OC为⊙O的半径,∴直线AB是⊙O的切线;
(2)连接OC,过E作EF⊥AB与F.

设⊙O的半径的半径为r,则OC=OD=r,∴OB=4+r.
∵BC=8,∠BCO=90°,∴![]() ,解得:r=6,∴OC=6,BO=10,BE=16.
,解得:r=6,∴OC=6,BO=10,BE=16.
∵OC⊥AB,EF⊥AB,∴OC∥EF,∴△OCB∽△EFB,
∴![]() ,即
,即![]() ,
,
∴EF=![]() ,BF=
,BF=![]() ,∴AF=
,∴AF=![]() ,∴AE=
,∴AE=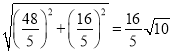 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当你把纸对折一次时,就得到2层,当对折两次时,就得到4层,照这样折下去(最多折7次).
(1)你能发现层数和折纸的次数有什么关系吗?
(2)计算当你对折6次时,层数是多少;
(3)如果纸的厚度是0.1 mm,求对折7次时,总厚度是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26 为①式,然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 为②式;②﹣ ①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2016(a≠0且a≠1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进价为60元,现在的售价为100元,每周可售出100件.市场调查发现:每降价1元,每周可多卖出20件.若设每件降价x元(x为整数),每周的销量为y件.
(1)请写出y与x之间的函数关系式;
(2)当售价定为多少时,每周的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,D是BC边上任意一点,以点A为中心,取旋转角等于∠BAC,把△ABD绕点A逆时针旋转得到△ACM.
(1)如图1,若∠BAC=50°,则∠BCM= ;
(2)如图2,在BC上取点E,使∠DAE=
 ∠BAC,求证:DE<BD+EC;
∠BAC,求证:DE<BD+EC;(3)如图3,在(2)的条件下,若∠BAC=90°,BD=1,EC=2,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与抛物线
与抛物线 相交于A
相交于A 和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.
和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.(1)求抛物线的解析式;
(2)在P点运动过程中,线段PQ的长是否存在最大值?若存在,求出这个最大值,并求出此时P点的坐标;若不存在,请说明理由;
(3)直线AB与y轴交于点C,与x轴交于点D,若△PBQ与△ODC相似,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径20,OP长为8,则过P的弦中,弦长为整数的弦共有( )条.
A.1 B.9 C.17 D.16
相关试题

