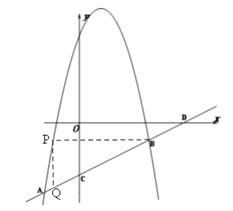
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A
相交于A![]() 和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.
和B(4,n)两点,点P是抛物线位于线段AB上方异于点A,B的一个动点,过点P作PQ⊥x轴,交线段AB于点Q.
(1)求抛物线的解析式;
(2)在P点运动过程中,线段PQ的长是否存在最大值?若存在,求出这个最大值,并求出此时P点的坐标;若不存在,请说明理由;
(3)直线AB与y轴交于点C,与x轴交于点D,若△PBQ与△ODC相似,求点P的坐标.

参考答案:
【答案】(1)![]() ;(2)线段PQ的长的最大值为9,此时P点坐标为(1,
;(2)线段PQ的长的最大值为9,此时P点坐标为(1, ![]() );(3)点P的坐标为(
);(3)点P的坐标为(![]() ,-1)或(
,-1)或(![]() ,6).
,6).
【解析】试题分析:(1)把A、B的坐标代入直线![]() ,即可得到m,n的值,从而得到A、B的坐标, 再把A、B的坐标代入抛物线的解析式,解方程即可得到结论;
,即可得到m,n的值,从而得到A、B的坐标, 再把A、B的坐标代入抛物线的解析式,解方程即可得到结论;
(2)设点P的横坐标为a,则P(a, ![]() ),Q(a,
),Q(a, ![]() ),用含a的代数式表示出PQ,配方即可得到结论;
),用含a的代数式表示出PQ,配方即可得到结论;
(3)分两种情况讨论:①当∠BPQ=90°时,②当∠PBQ=90°时.
试题解析:解:(1)∵A(m,-4)和B(4,n)在直线![]() 上,∴
上,∴![]() ,
, ![]() ,解得:m=-2,n=-1,∴A(-2,-4),B(4,-1), ∴
,解得:m=-2,n=-1,∴A(-2,-4),B(4,-1), ∴![]() ,解得:
,解得: 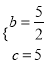 , ∴抛物线的解析式为
, ∴抛物线的解析式为![]() .
.
(2)设点P的横坐标为a,则P(a, ![]() ),Q(a,
),Q(a, ![]() ),
),
∴PQ=![]() ,∴当
,∴当![]() 时,线段PQ长取得最大值为9,此时P点坐标为(1,
时,线段PQ长取得最大值为9,此时P点坐标为(1, ![]() ).
).
(3)∵PQ∥y轴,∴∠PQB=∠OCD.
∵∠COD=90°,∴当∠PBQ=90°或∠BPQ=90°时,△PBQ与△ODC相似.
①当∠BPQ=90°时,PB∥x轴,∴P点的纵坐标为-1,由![]() 得:
得: ![]() 或
或![]() ,∴P(
,∴P(![]() ,-1);
,-1);
②当∠PBQ=90°时,设PB与x轴交于点M,由![]() 得:C(0,-3),D(6,0),∴OC=3,OD=6,∴CD=
得:C(0,-3),D(6,0),∴OC=3,OD=6,∴CD=![]() .
.
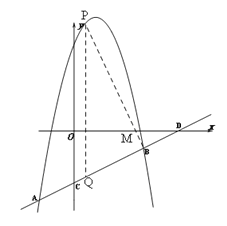
∵B(4,-1),∴BD=![]() .∵∠DBM=∠DOC=90°,∠BDM=∠ODC,∴△BDM∽△ODC,∴
.∵∠DBM=∠DOC=90°,∠BDM=∠ODC,∴△BDM∽△ODC,∴![]() ,即
,即![]() ,∴DM=
,∴DM=![]() ,∴OM=
,∴OM=![]() ,∴M(
,∴M(![]() ,0),∴直线PB的解析式为y=-2x+7.由
,0),∴直线PB的解析式为y=-2x+7.由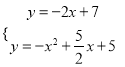 得:
得: ![]() ,
,  ,∴P(
,∴P(![]() ,6).
,6).
综上可知:点P的坐标为(![]() ,-1)或(
,-1)或(![]() ,6).
,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品进价为60元,现在的售价为100元,每周可售出100件.市场调查发现:每降价1元,每周可多卖出20件.若设每件降价x元(x为整数),每周的销量为y件.
(1)请写出y与x之间的函数关系式;
(2)当售价定为多少时,每周的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)如图2,直线BO与⊙O交于点D,E,若BD=4,AB=16,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,D是BC边上任意一点,以点A为中心,取旋转角等于∠BAC,把△ABD绕点A逆时针旋转得到△ACM.
(1)如图1,若∠BAC=50°,则∠BCM= ;
(2)如图2,在BC上取点E,使∠DAE=
 ∠BAC,求证:DE<BD+EC;
∠BAC,求证:DE<BD+EC;(3)如图3,在(2)的条件下,若∠BAC=90°,BD=1,EC=2,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径20,OP长为8,则过P的弦中,弦长为整数的弦共有( )条.
A.1 B.9 C.17 D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

相关试题

