Question

【题目】如图，已知直线和双曲线（k为正整数）交于A，B两点．

（1）当k=1时，求A、B两点的坐标；

（2）当k=2时，求△AOB的面积；

（3）当k=1时，△OAB的面积记为S1，当k=2时，△OAB的面积记为S2，…，依此类推，当k=n时，△OAB的面积记为Sn，若S1+S2+…+Sn=，求n的值．

Answer 1

【答案】（1） （2） （3）

【解析】试题分析：（1）由k=1得到直线和双曲线的解析式，组成方程组，求出方程组的解，即可得到A、B两点的坐标；（2）先由k=2得到直线和双曲线的解析式，组成方程组，求出方程组的解，即可得到A、B两点的坐标；再求出直线AB的解析式，得到直线AB与y轴的交点（0，2），利用三角形的面积公式，即可解答．（3）根据当k=1时，S1=×1×（1+2）=，当k=2时，S2=×2×（1+3）=4，…得到当k=n时，Sn=n（1+n+1）=n2+n，根据若S1+S2+…+Sn=，列出等式，即可解答．

试题解析：（1）当k=1时,直线y=x+k和双曲线化为：y=x+1和y= ，

解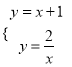得， ，

∴A(1,2),B(2,1)，

(2)当k=2时,直线y=x+k和双曲线化为：y=x+2和y=，

解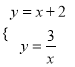得， ，

∴A(1,3),B(3,1)

设直线AB的解析式为：y=mx+n，

∴，

∴，

∴直线AB的解析式为：y=x+2

∴直线AB与y轴的交点(0,2)，

∴S△OB=×2×1+×2×3=4；

(3)当k=1时,S1=×1×(1+2)= ，

当k=2时,S2=×2×(1+3)=4，

…

当k=n时,Sn=n(1+n+1)= n2+n，

∵S1+S2+…+Sn=，

∴×(12+22+32+…+n2)+(1+2+3+…n)= ，

整理得： ×n(n+1)(2n+1)6+n(n+1)2=，

解得：n=6.