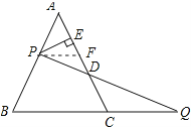
【题目】如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
(1)若∠Q=28°,求∠EPD的度数;
(2)求证:PD=QD.

参考答案:
【答案】(1)58°;(2)证明见解析.
【解析】试题分析:作PF∥BC交AC于F,先证明△APF是等边三角形,得出AP=AF=PF.证出PF=CQ,由ASA证明△PFD≌△QCD,得出对应边相等即可.
试题解析:(1)解:∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∵∠Q=28°,
∴∠EDP=∠CDQ=∠ACB﹣∠Q=32°,
∵PE⊥AC,
∴∠PED=90°,
∴∠EPD=90°﹣∠EDP=58°;
(2)证明:作PF∥BC交AC于F,如图所示:
∴∠APF=∠B=60°,∠AFP=∠ACB=60°,
∠FPD=∠CQD,∠PFD=∠QCD,
∴∠APF=∠AFP=∠A=60°,
∴△APF是等边三角形,
∴AP=AF=PF.
∵CQ=AP,
∴PF=CQ,
在△PFD和△QCD中,
∠FPD=∠CQD,PF=CQ,∠PFD=∠QCD
∴△PFD≌△QCD(ASA),
∴PD=QD.
-
科目: 来源: 题型:
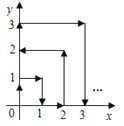
查看答案和解析>>【题目】一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,0)
B.(5,0)
C.(0,5)
D.(5,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”儿童节前夕,某幼儿园准备购买彩纸和拼图两种玩具,已知购买1盒彩纸和2盒拼图共需50元,购买2盒彩纸和3盒拼图共需80元.
(1)一盒彩纸和一盒拼图的价格各是多少元?
(2)该幼儿园准备购买这两种玩具共50盒(要求毎种产品都要购买),且购买总金额不能超过850元,至少购买彩纸多少盒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3a2=a6B.a8÷a2=a4C.a2+a2=a4D.(﹣a2)3=﹣a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
-
科目: 来源: 题型:
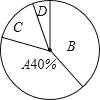
查看答案和解析>>【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级
成绩(分)
频数(人数)
频率
A
45~50
40
0.4
B
40~44
42
x
C
35~39
m
0.12
D
30~34
6
0.03
合计
1.00
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与y轴交于点C(0,3),与x轴交于点A、B,点A在点B的左边,且B(3,0),AB=2
(1)求该抛物线的函数关系式;
(2)如果抛物线的对称轴上存在一点P,使得△APC的周长最小,求此时P点的坐标,并求出△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.

相关试题

