【题目】观察表格:根据表格解答下列问题:
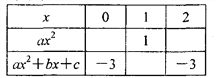
(l) a=______,b=_____,c=_____;
(2) 在右图的直角坐标系中画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c > -3成立;
(3)该图象与x轴两交点从左到右依次分别为A、B,与y轴交点为C,求过这三个点的外接圆的半径.
参考答案:
【答案】 1 -2 -3
【解析】试题分析:(1)直接将![]() 代入求出
代入求出![]() 即可,进而将
即可,进而将![]() 代入求出
代入求出![]() ,再分别将
,再分别将![]() 代入求出
代入求出![]() 的值;
的值;
(2)再利用函数解析式进而得出函数图象,进而得出不等式的解集.
(3)根据题意求得外接圆的圆心的坐标为![]() ,进而求得圆的半径.
,进而求得圆的半径.
试题解析:(1) ![]() 过(1,1),
过(1,1),
∴1=a,
∴当x=2时, ![]()
![]() 过(0,3),(2,3),a=1,
过(0,3),(2,3),a=1,
![]()
解得:b=2,
![]() 当x=1时,y=4,
当x=1时,y=4,
故答案为:1,2,3;
(2)如图所示:当![]() 或
或![]() 时,不等式
时,不等式![]()
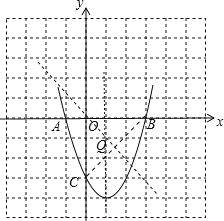
(3)由(2)可知A(1,0),B(3,0),C(0,3),
则作BC、AB的垂直平分线的交点Q(1,1),
∴外接圆的半径![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点M(1,4),N(5,2),P(0,3),Q(3,0),过P,Q两点的直线的函数表达式为y=﹣x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为ts.
(1)若直线PQ随点P向上平移,则:
①当t=3时,求直线PQ的函数表达式.
②当点M,N位于直线PQ的异侧时,确定t的取值范围.
(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.
(3)若点P向上移动,点Q不动.若过点P,Q的直线经过点A(x0,y0),则x0,y0需满足什么条件?请直接写出结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年共有
 万名考生参加中考,为了了解这
万名考生参加中考,为了了解这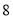 万名考生的数学成绩,从中抽取了
万名考生的数学成绩,从中抽取了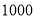 名考生的数学成绩进行统计分析,以下说法正确的有( )
名考生的数学成绩进行统计分析,以下说法正确的有( )①这种调查采用了抽样调查的方式;②这种调查采用了全面调查的方式;③
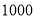 是样本容量;④每名考生的数学成绩是个体
是样本容量;④每名考生的数学成绩是个体A.
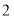 B.
B. 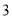 C.
C. 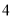 D.
D. 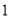
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极响应市委政府“加快建设美丽江城”的号召,我市某街道决定从备选的五种树中选购--种进行栽种。为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

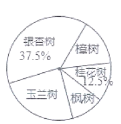
请根据所给信息解答以下问题:
(1)这次参与调查的居民总人数是多少人?
(2)此次调查的居民中最喜欢樟树的有多少人?请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, ,
, 、
、 相交于点
相交于点 ,
, 于点
于点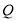 ,
, ,
, .
.(1)求证:
 ;
;(2)求
 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车去韶山研学, 现有甲、乙两种大客车,甲种客车每辆载客量
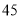 人,乙种客车每辆载客量
人,乙种客车每辆载客量 人.已知
人.已知 辆甲种客车和
辆甲种客车和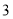 辆乙种客车需租金
辆乙种客车需租金 元,
元,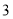 辆甲种客车和
辆甲种客车和 辆乙种客车共需租金
辆乙种客车共需租金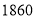 元.
元.(1)求
 辆甲种客车和
辆甲种客车和 辆乙种客车的租金分别是多少元?
辆乙种客车的租金分别是多少元?(2)学校计划租用甲、乙两种客车共
 辆,送
辆,送 名师生集体外出活动,总费用不超过
名师生集体外出活动,总费用不超过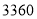 元,则共有哪几种租车方案?
元,则共有哪几种租车方案?
相关试题

