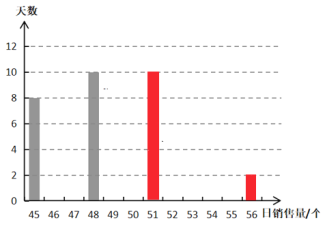
【题目】某面包店推出一款新口味面包,每个成本1.5元,售价5元/个,试营业期间一律8折,每天只生产50个,为保持面包新鲜,当天未卖完的当天销毁,试营业期间市场日需求量(即每天所需数量)如表所示:
天数 | 8 | 10 | 10 | 2 |
日需求量/个 | 45 | 48 | 51 | 56 |
(1)补充日销售量(即每天销售的数量)的条形统计图;
(2)试营业期间某天的日需求量为45个,求当天的利润;
(3)求试营业期间(30)天的总利润

参考答案:
【答案】(1)见解析;(2)105元;(3)3510元.
【解析】
(1)根据表格提供的数据补全条形统计图即可;
(2)先求出在试营业期间每个面包的利润,再求45个面包的总利润,其中要减去5个没卖出的成本即可;
(3)根据表格提供的数据扣除多生产的成本即可求出30天的总利润.
(1)根据表格提供的数据,补全图形如下;
(2)45×(5×0.8-1.5)=112.5(元).
112.5-1.5×5=105(元),
故当天的利润为105元.
(3)每个面包的利润为:5×0.8-1.5=2.5(元),
试营业期间(30)天的总利润=45×2.5×8+48×2.5×10+50×2.5×10+50×2.5×2-1.5×5×8-2×1.5×10=3510(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是
 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28,∠AGF=80,FH平分∠EFG.
(1)说明:DC∥AB;
(2)求∠PFH的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解不等式2(1﹣x)<5﹣3x
(2)求不等式
 的正整数解
的正整数解(3)解不等式组
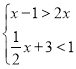
(4)解不等式组
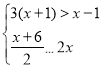 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为
 ,
, ,
, ,…,
,…,  ,则
,则 = .
= . 
相关试题

