【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
参考答案:
【答案】(1)z=-2x2+136x-1800;(2)当销售单价为34元时,每月能获得最大利润,最大利润为512万元;(3)每月最低制造成本为648万元
【解析】(1)根据每月的利润z=(x-18)y,再把y=-2x+100代入即可求出z与x之间的函数解析式;
(2)把z=350代入z=-2x2+136x-1800,解这个方程即可,将z═-2x2+136x-1800配方,得z=-2(x-34)2+512,即可求出当销售单价为多少元时,厂商每月能获得最大利润,最大利润是多少.
(3)结合(2)及函数z=-2x2+136x-1800的图象即可求出当25≤x≤43时z≥350,再根据限价32元,得出25≤x≤32,最后根据一次函数y=-2x+100中y随x的增大而减小,即可得出当x=32时,每月制造成本最低,最低成本是18×(-2×32+100)
解:(1)z=(x-18)y=(x-18)(-2x+100)
=-2x2+136x-1800,
∴z与x之间的函数解析式为z=-2x2+136x-1800;
(2)由z=350,得350=-2x2+136x-1800,
解这个方程得x1=25,x2=43
所以,销售单价定为25元或43元,
将z═-2x2+136x-1800配方,得z=-2(x-34)2+512,
答;当销售单价为34元时,每月能获得最大利润,最大利润是512万元;
(3)结合(2)及函数z=-2x2+136x-1800的图象(如图所示)可知,

当25≤x≤43时z≥350,
又由限价32元,得25≤x≤32,
根据一次函数的性质,得y=-2x+100中y随x的增大而减小,
∵x最大取32,
∴当x=32时,每月制造成本最低.最低成本是18×(-2×32+100)=648(万元),答:每月最低制造成本为648万元.
“点睛”本题考查的是二次函数在实际生活中的应用,关键是根据题意求出二次函数的解析式,综合利用二次函数和一次函数的性质解决实际问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(2x+1)(x﹣1)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把弯曲的河道改成直的,可以缩短航程,其理由是( )
A. 经过两点有且只有一条直线
B. 两点之间,线段最短
C. 两点之间,直线最短
D. 线段可以比较大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了打造风光带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m.求甲、乙两个工程队分别整治了多长的河道.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
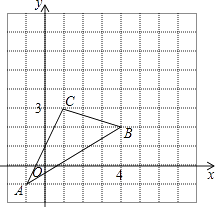
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,请在图中画出△A′B′C′,并写出点A′、B′、C′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
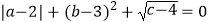
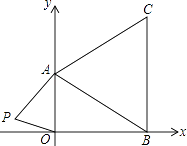
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m, ),请用含m的式子表示四边形ABOP的面积;
),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x(3x﹣4)+2x(x+7)=5x(x﹣7)+90.
相关试题

